EQSLV
Main Menu > Solution> Analysis Option .
Каждая из этих опций подробно обсуждается далее.
Опция New Analysis используется, если вам необходимо приложить новую гармоническую силу.
Опция Harmonic Response определяет тип анализа- гармонический анализ.
Опция метод решения позволяет вам выбрать один из следующих методов:
Полный метод (Fool method);
Усеченный метод (Reduced method);
Метод суперпозиции мод (Mode superposition method).
Опция формат вывода (Solution Listing Format) позволяет определить как гармонические перемещения будут выводиться на печать (Jobname.OUT). Вы можете выбрать, чтобы выводилась действительная и мнимая часть, или амплитуда и фазовый угол.
Опция вид матрицы масс (LUMPM).
Эта опция используется по умолчанию или соответствует аппроксимации матрицы масс сосредоточенными массами (в этом случае матрица масс имеет диагональный вид). Мы рекомендуем значение этой опции принимать по умолчанию для большинства приложений. Для некоторых задач, использующих “тонкие” системы, такие, как тонкие балки или очень тонкие оболочки, аппроксимация матрицы масс с помощью сосредоточенных масс часто приводит к лучшим результатам. Аппроксимация матрицы масс при помощи сосредоточенных масс требует меньшего времени решения и памяти.
После заполнения всех полей диалогового «ящика» опций гармонического анализа нажмите на кнопку «ОК» и появится второй диалоговый «ящик», где вы выберете метод решения.
Опция «Метод решения» [EQSLV]. Вы можете выбрать фронтальный метод (по умолчанию), метод соединенных градиентов Якоби (JCG), метод неполных соединенных градиентов Холецкого (ICCG). Фронтальный метод рекомендуется для большинства задач механики.
3. Приложение нагрузок к модели.
Гармонический анализ по определению предполагает, что приложенные нагрузки изменяются по синусоидальному закону по времени. Для полного описания гармонических нагрузок используется три параметра: амплитуды, фазовые углы, частотный диапазон (рис 2.1).
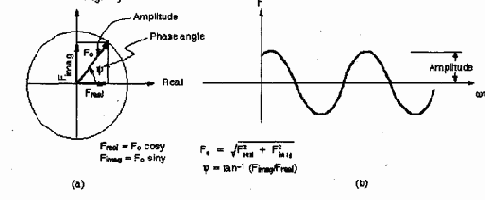 |
Амплитуда – это максимальное значение нагрузки, которые выбираются с использованием команд, приведенных в таблице 2.2.
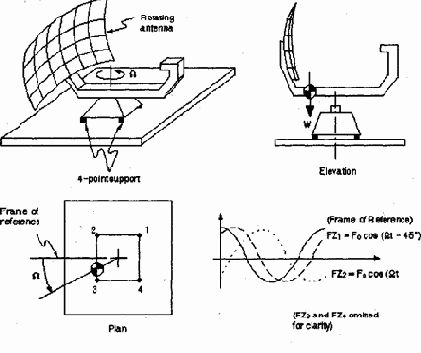
Фазовый угол – это измеренное время, на которое нагрузка запаздывает или опережает относительно заданного момента времени. На комплексной диаграмме (см. рис 2.1) этот угол измеряется относительно действительной оси. Фазовый угол требуется только в том случае, если имеется несколько нагрузок, отличающихся по фазам. Например, вращение неуравновешенной антенны, показанной на рис. 2.2 будет приводить к вертикальным нагрузкам в четырех опорных точках с различными фазовыми углами.
 |
Первый временной шаг в приложенной нагрузке используется для установки начальных условий, т. е. при t=0. Динамический анализ переходных процессов требует два набора начальных условий (так как уравнения движения представляют собой уравнения второго порядка): начальные перемещения



Нулевые начальные перемещения и нулевые начальные скорости - это начальные условия по умолчанию, т.е. если

Ненулевые начальные перемещения и ненулевые начальные скорости вы можете ввести такие начальные условия с помощью команды IC или через интерфейс:
Main Menu>Solution>-Loads Apply>Initial Condit`n>Define
Предостережение: Нельзя определять несовместные начальные условия. Например, вы определили начальную скорость в единственной степени свободы, а начальная скорость во всех других степенях свободы равна нулю, что приводит к конфликту начальных условий. В большинстве случаев начальные условия вводятся во всех незакрепленных степенях свободы модели. Если эти начальные условия не одинаковы для всех степеней свободы, то нужно вводить их, как показано ниже. (См. описание команд TIMIND и IC).
Нулевые начальные перемещения и ненулевые начальные скорости Ненулевые скорости вводятся приложением малых перемещений в течение малого временного интервала на части конструкции, где должна быть определена скорость. Например, если

TININT, OFF |Эффект временного интегрирования выключен
D, ALL, UY, 0.001 |Введены малые перемещения (скорость направлена по Y )
TIME, 0.004 | начальная скорость =0,001/0,004=0,25
LSWRITE | Запись данных в файл шагов нагрузки (Jobname.S01)
DDELE, ALL, UY| Уничтожение приложенных перемещений
TININT, ON |Эффект временного интегрирования включен
Ненулевые начальные перемещения и ненулевые начальные скорости
Это тот же случай, что приведен выше, исключая то, что вместо малых перемещений вводятся их действительные значения. Например, если


TININT, OFF |Эффект временного интегрирования выключен
D, ALL, UY, 1.0 |Введены перемещения (скорость направлена по Y )
TIME, 0.4 | начальная скорость =1.0/0,4=2,5
LSWRITE | Запись данных в файл шагов нагрузки (Jobname.S01)
DDELE, ALL, UY| Уничтожение приложенных перемещений
TININT, ON |Эффект временного интегрирования включен
Ненулевые начальные перемещения и нулевые начальные скорости
Это требует использования двух шагов [NSUBST,2] с шагом изменения выбранных перемещений [KBS,1]. Без шага изменения заданные перемещения будут изменяться непосредственно со временем, приводя к ненулевой начальной скорости. Пример, приведенный ниже, показывает, как ввести


TININT, OFF |Эффект временного интегрирования выключен
D, ALL, UY, 1.0 |Введены перемещения (скорость направлена по Y )
TIME, 0.001 | Малый временной интервал
NSUBST, 2 |Два шага
KBC,1 | Скачек нагрузки
LSWRITE | Запись данных в файл шагов нагрузки (Jobname.S01)
Анализ переходного процесса
TIMINT,ON | Эффект временного интегрирования включен
TIME,…. | Реальный временной шаг
DDELE, ALL, UY| Удаление заданных перемещений
KBC,0 |Плавно возрастающая нагрузка (если нужно)
Продолжение процедуры нормального переходного анализа
Ненулевое начальное ускорение
Это может быть аппроксимировано выбором требуемого ускорения [ACEL] в малый интервал времени. Команды, применяемые для ввода начального ускорения 9,81, приведены ниже.
ACEL,,9.81 | Начальное ускорение в Y направлении
TIME, 0.001 | Малый временной интервал
NSUBST,2 | Два шага
KBS,1 |Скачек нагрузки
LSWRITE | Запись данных в файл шагов нагрузки (Jobname.S01)
Переходный анализ
TIME,….| Реальный временной шаг
DDELE,.. | Удаление заданных перемещений (если требуется)
KBC,0 | Плавно возрастающая нагрузка (если нужно)
Продолжение процедуры нормального переходного анализа
Приложение нагрузок для динамического анализа переходных процессов
В таблице 6.2 приведены возможные нагрузки для динамического анализа переходных процессов. Выбирая инерционные нагрузки, вы можете определить их и для твердотельной модели, и для конечно-элементной модели. Вы можете также определить сложные граничные условия массивом табличного типа.
Таблица 6.2
Нагрузки для переходного анализа
|
Тип нагрузки |
Категория |
Команды |
Интерфейс |
|
Перемещения (UX, UY, UZ, ROTX, ROTY, ROTZ |
Закрепления |
D |
Main Menu>Solutions>-Loads-Apply-Stuctural-Displasiment |
|
Силы, моменты (FX, FY, FZ, MX, MY, MZ) |
Силы |
F |
Main Menu>Solutions>-Loads-Apply-Stuctural-Forse/Moment |
|
Давление (PRES) |
Поверхностные нагрузки |
SF |
Main Menu>Solutions>-Loads-Apply-Stuctural-Pressure |
|
Температура (TEMP) Обтекание (FLUE) |
Объемные нагрузки |
BF |
Main Menu>Solutions>-Loads-Apply-Stuctural-Temperature |
|
Гравитация, вращение |
Инерционные нагрузки |
- |
Main Menu>Solutions>-Loads-Apply-Stuctural-Other |
В таблице 6.3 приведены команды приложения нагрузок для динамического анализа переходных процессов.
Таблица 6.3
|
Тип нагрузки |
Тведотельная или конечно-элементная модель |
Объекты |
Приложение |
Удаление |
Печать |
Операции |
Опции |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Перемещения |
Твердотельная |
Точки |
DK |
DKDELE |
DKLIST |
DTRAN |
- |
|
Твердотельная |
Линии |
DL |
DLDELE |
DLLIST |
DTRAN |
- |
|
|
Твердотельная |
Поверхности |
DA |
DADELE |
DALIST |
DTRAN |
- |
|
|
Конечно-элементная |
Узлы |
D |
DDELE |
DLIST |
DSCALE |
DSYM DSUM |
|
|
Силы |
Твердотельная |
Точки |
FK |
FKDELE |
FKLIST |
FTRAN |
- |
|
Конечно-элементная |
Узлы |
F |
FDELE |
FLIST |
FSCALE |
FSUM |
|
|
Давление |
Твердотельная |
Линии |
SFL |
SFLDELE |
SFLLIST |
SFTRAN |
SFGRAD |
|
Твердотельная |
Поверхности |
SFA |
SFADELE |
SFALIST |
SFTRAN |
SFGRAD |
|
|
Конечно-элементная |
Узлы |
SF |
SFDELE |
SFLIST |
SFSCALE |
SFGRAD SFCUM |
|
|
Конечно-элементная |
Элементы |
SFE |
SFEDELE |
SFELIST |
SFSCALE |
SFGRAD SFBEAM SFFUN SFCUM |
Продолжение табл.6.3
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Температура, Обтекание |
Твердотельная |
Точки |
BFK |
BFKDELE |
BFKLIST |
BFTRAN |
- |
|
Твердотельная |
Линии |
BFL |
BFLDELE |
BFLLIST |
BFTRAN |
- |
|
|
Твердотельная |
Поверхности |
BFA |
BFADELE |
BFALIST |
BFTRAN |
- |
|
|
Твердотельная |
Объемы |
BFV |
BFVDELE |
BFVLIST |
BFTRAN |
- |
|
|
Конечно-элементная |
Узлы |
BF |
BFDELE |
BFLIST |
BFSCALE |
BFSUM |
|
|
Конечно-элементная |
Элементы |
BFE |
BFEDELE |
BFELIST |
BFSCALE |
BFSUM |
|
|
Инерционные |
- |
- |
ACEL OMEGA DOMEGA CGLOC CGOMGA DCGOM IRLF |
- |
- |
- |
- |
Приложение нагрузок на линии.
Main Menu>Solutions>-Loads-Apply-Stuctural-Displasiment>On Lines
Печать нагрузок
Utility Menu>List>Loads>Load type
Возможные опции шагов нагрузки для динамического анализа переходных процессов приведены в таблице 6.4.
Таблица 6.4
|
Опция |
Команда |
Действия в интерфейсе |
|
Динамические опции |
||
|
Эффект интегрирования по времени |
TIMINT |
Main Menu>Solutions>-Loads Step Opt-Time/Frequense > Time Integration |
|
Переходные параметры интегрирования |
TINTP |
Main Menu>Solutions>-Loads Step Opt-Time/Frequense > Time Integration |
|
Демпфирование |
ALPHAD BETAD MP,DAMP |
Main Menu>Solutions>-Loads Step Opt-Time/Frequens > Damping |
|
Основные опции |
||
|
Время |
TIME |
Main Menu>Solutions>-Loads Step Opt-Time/Frequens > Time & Time Step или Time & Substep |
|
Скачкообразная или плавно изменяющаяся нагрузка |
KBC |
Main Menu>Solutions>-Loads Step Opt-Time/Frequens > Time & Time Step или Time & Substep |
