Демпфирование используется только для комбинаций
|
Модальный Без демпфирования Модальный с демпфированием |
Нет5 Да |
Нет5 Да |
Нет5 Да |
Нет Да |
Нет Да |
|
Гармонический Полный Усеченный Супер. Поз Мод |
|||||
|
Да |
Да |
Да |
Нет |
Да |
|
|
Да |
Да |
Да |
Нет |
Да |
|
|
Да |
Да4 |
Да |
Да |
Нет |
|
|
Переходный Полный Редуцированный Супер. Поз Мод |
|||||
|
Да |
Да |
Нет |
Нет |
Да |
|
|
Да |
Да |
Нет |
Нет |
Да |
|
|
Да |
Да4 |
Да |
Да |
Нет |
|
|
Спектральный SPRS MPRS2 |
Да1 |
Да |
Да |
Да |
Нет |
|
DDAM |
Да1 |
Да |
Да |
Да |
Нет |
|
PSD |
Да |
Нет |
Да |
Да |
Нет |
|
Устойчивость |
Нет |
Нет |
Нет |
Нет |
Нет |
|
Подконструкции |
Да |
Да |
Нет |
Нет |
Да |
Примечание к таблице 7.1
1. Только b демпфирование
2. Демпфирование используется только для комбинаций мод, а не для расчета коэффициентов мод.
3. Включая матрицу демпфирования суперэлемента.
4. Если преобразуется к модальному демпфированию раскрытием мод
5. Эффективное отношение демпфирования определяется для спектрального анализа.
Альфа и бета демпфирование применяется для определения матрицы демпфирования по Рэлею. Матрица демпфирования определяется с использованием матрицы масс и матрицы жесткости:

Команды ALPHAD и BETAD используются для определения a и b как десятичных чисел. Значения a и b, как правило, не известны заранее, но они могут быть определены из коэффициентов модального демпфирования




Во многих практических случаях альфа демпфирование (или массовое демпфирование) может игнорироваться (a=0). В этих случаях вы можете определить b из известных значений



Для определения коэффициентов a и b при заданном отношении демпфирования x обычно принимается, что сумма a и b членов примерно постоянна в частотном диапазоне.(Рис. 7.2). Таким образом, при данной x и частотном диапазоне от


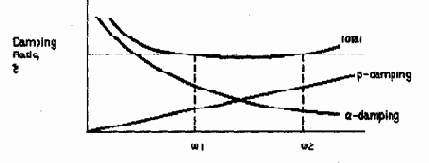 |
Альфа демпфирование может приводить к неверным результатам, если большая масса была искусственно введена в модель. Один общий пример, когда искусственно большая масса вводится в основание модели для возможности ввода спектра ускорений. (Вы можете использовать большие массы для преобразования спектра ускорений в спектр сил). Демпфирующий коэффициент альфа, который умножается на матрицу масс, будет давать искусственно завышенную силу демпфирования в таких системах, что приводит к ошибкам во входном спектре и в определении реакции системы.
Бета демпфирование и демпфирование материала может приводить к искаженным результатам в нелинейном анализе. Эти коэффициенты демпфирования умножаются на матрицу жесткости, которая постоянно изменяется в нелинейных задачах. Результирующее изменение в демпфировании может быть иногда противоположным действительному изменению демпфирования, что может исказить физическую сущность задачи. Например, из опыта известно, что в физических системах, которые размягчаются при пластической деформации, обычно соответственно повышается демпфирование при развитии пластического течения. В модели ANSYS, имеющей бета демпфирование, будет снижение демпфирования при развитии пластической деформации.
Демпфирование, зависящее от свойств материала, позволяет вам определять бета демпфирование как свойства материала [MP,DAMP]. Следует отметить, что в спектральном анализе вводится демпфирующее отношение, зависящее от свойств материала x, а не b. Еще отметим, что для элементов, в которых возможны несколько материалов, такие, как SOLID46, SOLID65, SHELL91, SHELL99, b может быть определен для всего элемента, а не для каждого материала в элементе. В этом случае b определяется из свойств материалов элементов с помощью команды MAT.
Постоянное отношение демпфирования – наиболее простой путь определения демпфирования для системы. Он представляет собой отношение действительного демпфирования к критическому значению и вводится как десятичная дробь командой DMPRAT. Это возможно только в спектральном анализе, гармоническом анализе и в методе суперпозиции мод в анализе переходных процессов.
Модальное демпфирование
дает вам возможность вводить различное отношение демпфирования для различных мод колебаний. Это возможно только спектрального анализа и для метода методе суперпозиции мод в анализе переходных процессов.
Демпфирование элементов вводится для элементов с вязким демпфированием, таких как COMBIN7, COMBIN14, COMBIN37, COMBIN40 и т. д.
8. СПЕКТРАЛЬНЫЙ АНАЛИЗ.
Спектральный анализ – это решение задачи с использованием результатов модального анализа для расчета перемещений и напряжений в модели. Он в основном используется вместо временного анализа для определения реакции при случайных нагрузок или нагрузках, зависящих от времени, таких как землетрясение или ветровые нагрузки, нагрузки от морских волн, воздействие от реактивного двигателя, и т. д.
Спектр это график спектральной величины в функции от частоты, что определяет интенсивность и спектральный состав динамических нагрузок. Возможны три типа спектрального анализа:
Спектр реакции;
-Единственный спектр реакции (SPRS)
-Множественный спектр реакции (MPRS)
Метод динамического проектирования (DDAM)
Метод спектральной плотности мощности (PSD).
8.1 Виды спектрального анализа.
8.1.1 Спектр реакции.
Спектр реакции представляет реакцию систем с одной степенью свободы, на нагрузку, зависящую от времени. Это график реакции в функции от частоты, где в качестве реакции может быть принято перемещение, скорость, ускорение или сила. Возможны два типа спектрального анализа реакции: единственный спектр реакции и множественный тип реакции.
При анализе
единственного спектра реакции вы выбираете одну спектральную кривую (или семейство кривых) в ряде точек модели, например в опоре.
При анализе множественного спектра реакции вы выбираете различные спектральные кривые в различных точках.
8.1.2 Метод динамического проектирования.
Метод динамического проектирования – это технология, используемая для оценки ударной сопротивляемости судового оборудования. Технология по существу является спектральным анализом реакции, в котором спектр получается из серии эмпирических уравнений и ударных проектных таблиц, полученных в Американской Национальной исследовательской лаборатории. Отчет NRL-1396.
8.1.3 Метод спектральной плотности.
Спектральная плотность мощности – это статистическая величина, для которой в качестве предела определена среднеквадратичная величина случайной переменной. Она используется в анализе случайной вибрации, в котором мгновенное значение реакции может быть определено только по функции вероятностного распределения, показывающей вероятность нахождения случайной величины в некотором интервале.
График спектральной плотности может строиться в функции частоты для перемещения, скорости, ускорения или силы. Математически, площадь под кривой равна дисперсии (или среднему квадрату).
8.2 Последовательность действий при решении задачи спектрального анализа.
1. Построение модели
2. Получение модального решения
3. Получение спектрального решения
4. Расширение мод
5. Комбинация мод
6. Просмотр результатов.
Модальное решение должно быть получено перед расчетом спектра, формы мод и частоты используются в спектральном анализе. Производя спектральное решение перед раскрытием мод, вы можете раскрыть только те моды, которые требуются для финального решения.
Построение модели.
В этом шаге вы определяете имя задачи, заголовок задачи, затем используя препроцессор определяете тип элементов, реальные константы, свойства материалов и геометрию модели.
Учитывается только линейное поведение в спектральном анализе. Нелинейные элементы (если они есть) представляются как линейные. Например, если вы включаете контактные элементы, их жесткость рассчитывается на начальном этапе, и не изменяется.
Модуль упругости (или жесткость в некоторой форме) и плотность (или масса) должны быть обязательно заданы. Свойства материала могут быть линейные, изотропные или ортотропные, постоянные или зависящие от температуры, но нелинейные свойства игнорируются.
Получение модального решения.
Собственные частоты и формы мод необходимы для получения спектрального анализа.
Используйте метод подпространства, блочный или редуцированный. Другие методы не подходят для спектрального анализа.
Число полученных мод должно быть достаточным для характеристики реакции системы в интересующем вас частотном диапазоне.
Если вы используете метод интерфейса, выбирайте NO на диалоговом меню раскрытия мод [MODOPT], так что моды не раскроются в это время, но могут быть раскрыты отдельно в соответствующем шаге решения. В этом случае нужно выбирать YES для раскрытия всех мод.
Если вы используете демпфирование, зависящее от свойств материалов, вы должны это выбрать в модальном анализе.
Необходимо закрепить те степени свободы, где вы хотите приложить входной спектр основания.
Получение спектрального решения.
Файл формы мод (Jobname.MODE) из модального анализа должен быть получен и база данных должна содержать данные этой модели.
1. Войдите в режим решения:
Команда /SOLU или интерфейс Main Menu>Solutions
2. Определите тип анализа и его опции.
Таблица 8.1
Тип анализа и опции
|
Опции |
Команды |
Действия в интерфесе |
|
New Analysis |
ANTYPE |
Main Menu>Solutions>Analys Type>New Analys |
|
Analys Type: Spectrum |
ANTYPE |
Main Menu>Solutions>Analys Type>New Analys>Spectrum |
|
Тип спектра:SPRS |
SPOPT |
Main Menu>Solutions>Analys Options |
|
Число мод для решения |
SPOPT |
Main Menu>Solutions>Analys Options |
Точность решения существенно зависит от числа используемых мод: чем больше число мод, тем выше точность.
3. Определите опции шагов нагрузки. Возможны следующие опции для однофакторного спектрального анализа.
Опции шагов нагрузки
Таблица 8.2
|
Опция |
Команда |
Действия в интерфейсе |
|
|
Опции спектра |
|||
|
Тип спектра реакции |
SVTVP |
Main Menu>Solutions>Load Step Opt-Spectrum>Single-point-Settings |
|
|
Направление возбуждения |
SED |
Main Menu>Solutions>Load Step Opt-Spectrum>Single-point-Settings |
|
|
Зависимость спектра от частоты (спектральная кривая) |
FREQ, SV |
Main Menu>Solutions>Load Step Opt-Spectrum>Single-point-Freq Table/Spectr Values |
|
|
Демпфирование (динамические опции) |
|||
|
Бета (демпфирование, пропорциональное жесткости |
BETAD |
Main Menu>Solutions>Load Step Opt>Time/Frequens>Damping |
|
|
Постоянное отношение демпфирования |
DMPRAT |
Main Menu>Solutions>Load Step Opt>Time/Frequens>Damping |
|
|
Модальное демпфирование |
MDAMP |
Main Menu>Solutions>Load Step Opt>Time/Frequens>Damping |
|
Опции спектра содержат следующее:
Тип спектра [SVTYP].
Тип спектра может быть перемещение, скорость, ускорение, сила или спектральная плотность. Все спектры за исключением силы представляют собой сейсмически спектры и действуют на опорах. Спектр силы прикладывается на не опорных узлах с помощью команд F или FK и по направлению меток FX, FY, FZ. Спектральная плотность [SVTYP,4] внутренне преобразовывается в спектр перемещений и ограничивается шириной полосы частот.
Направление воздействия.
Спектральная кривая [FREQ, SV].
Команды FREQ, SV используются для определения спектральной кривой. Вы можете определить семейство спектральных кривых, каждая кривая для различного отношения демпфирования. Используйте команду STAT для печати текущих значений кривых. Другая команда ROCK позволяет вам определить спектр качаний.
Демпфирование (динамические опции).
Если вы выбрали более, чем одну форму демпфирования, ANSYS будет рассчитывать эффективное отношение демпфирования на каждой частоте. Спектральное значение этого эффективного отношения демпфирования будет затем рассчитываться методом интерполяции на спектральной кривой. Если демпфирование не определено, будет использоваться спектральная кривая с наивысшим демпфированием.
4. Запустите решение.
Main Menu>Solution>Solve-Current LS
Выход решения включает таблицу действующих факторов. Таблица действующих факторов содержит коэффициенты мод (принятых по наинизшему отношению демпфирования) и распределение масс для каждой моды. Для получения максимальной реакции каждой моды (модальной реакции) нужно умножить форму моды на модальный коэффициент. Вы можете сделать это восстановлением коэффициентов мод командой GET и использованием их в качестве масштабного фактора в команде SET.
5. Повторите шаги 3 и 4 для дополнительных спектров реакции, если это необходимо. Заметим, что решение не записывается в файл с расширением RST в это время.
6. Выйдите из процессора.
8.3 Расширение мод.
1. Нажмите на кнопку «YES» на диалоговом окне расширения мод (Expansion Pass).
Команда MXPAND.
Интерфейс: Main Menu>Solution>New Analys-Modal Expansion Pass-On > L.S Opt-Expansion Pass>Single Expand-Modal-Expand Modes
Вы должны раскрывать моды, не зависимо от того, какой метод используется: подпространства, блочный или редуцированный.
Селективно раскрыты, могут быть только значительные моды. (См. использование поля SIGNIF в команде MXPAND). Если вы используете интерфейс и хотите выборочно раскрыть моды, Выберите «NO» в диалоговом окне раскрытия мод для опций модального анализа [MODOPT].
Только раскрытые моды используются для операции комбинации мод.
Если вас интересуют напряжения, вы должны здесь запросить расчет напряжений. По умолчанию, напряжения не определяются при раскрытии мод, это означает, что напряжения не определяются для спектрального анализа.
Если вы хотите раскрыть все моды, вы можете включить шаг раскрытия мод в модальном анализе командой MXPAND. Если вы используете интерфейс и хотите раскрыть все моды, выберите «YES» в диалоговом окне для модального анализа. Но если вы хотите раскрыть только значительные моды вы должны рассматривать раскрытие мод как отдельное решение после спектрального анализа. Заметим, что решение модального анализа записывается в результирующий файл Jobname.RST, только если раскрытие мод закончено.
8.4 Комбинирование мод.
1. Войдите в режим «решение».
Main Menu>Solutions.
2. Определите тип анализа.
Main Menu>Solutions>Analys Type>New Analys
Выберите тип анализа «spectrum»
3. Выберите один из способов метода комбинаций мод для спектрального анализа:
Квадратный корень из суммы квадратов (SRSS);
Полная квадратичная комбинация (CQC);
Двойная сумма (DSUM);
Группирование (GRP);
Суммирование по способу военно-морской исследовательской лаборатории. (NRLSUM).
Для определения метода комбинаций мод используются команды:
SRSS
CQC
DSUM
GRP
NRLSUM
Интерфейс: Main Menu>Solution>New Analys->Spectrum >Analysis Opt-SPRS> Load Step Opt-Spectrum>Spectrum-Single Point-Mode Combin.
Эти команды позволяют считать различные типы реакций:
Перемещение (метка=DISP);
Скорость (метка =VELO);
Ускорение (метка =ACEL)
Примечание: вы должны определить демпфирование, если вы используете метод CQC.
4. Запустите решение.
Main Menu>Solution>Solve-Current LS
Результаты решения записываются в файл Jobname.MCOM Чтение этого файла в постпроцессоре POST1 производится с использованием Jobname.RST из шага раскрытия мод. Файл Jobname.MCOM содержит команды POST1, комбинирующие максимальные модальные реакции с использованием выбранного способа комбинирования мод для расчета предельных реакций системы.
Если вы выбрали перемещение в качестве типа реакции, то перемещения и напряжения комбинируются для каждой моды;
Если вы выбрали скорость в качестве типа реакции, то скорость и напряжения комбинируются для каждой моды;
Если вы выбрали ускорение в качестве типа реакции, то ускорения и напряжения комбинируются для каждой моды;
5. Выйдите из процессора.
8.5 Просмотр результатов.
Результаты спектрального анализа записываются в файл Jobname.MCOM в форме команд постпроцессора POST1. Эти команды рассчитывают предельные реакции системы комбинацией максимальных модальных реакций в некотором виде ( в соответствии с выбранным методом). Предельные реакции состоят из предельных перемещений (или скоростей или ускорений), и если помещены в результирующий файл при шаге раскрытия мод, предельные напряжения, деформации и силы реакции.
Вы можете использовать генеральный постпроцессор POST1 для просмотра результатов.
Примечание: Если вы хотите непосредственно комбинировать действующие напряжения (S1, S2, S3, SEQV, SI) из результирующего файла, введите команду SUMTYPE, PRIN перед чтением файла Jobname.MCOM.
1. Прочтите команды из файла Jobname.MCOM.
Команда /INPUT, например, /INPUT,FILE,MCOM.
Интерфейс: Utility Menu>File>Read Input From
2. Просмотрите результаты.
Опция: просмотр деформированного состояния.
Команда PLDISP.
Интерфейс: Main Menu>General Postproc>Plot Results>Deformed Shape.
Опция просмотр результатов в контурном виде.
Команды PLNSOL или PLESOL.
Интерфейс: Main Menu> General Postproc>Plot Results> Contour Plot>Nodal Solu или Element Solu.
Опция просмотр результатов в векторном виде.
Команда PLVEC
Интерфейс: Main Menu> General Postproc>Plot Results> Vector Plot>Predefined
Опция табулированный листинг.
Команды: PRNSOL (решение в узлах);
PRESOL (решение в элементах);
PRRSOL (Силы реакции).
Интерфейс:
Main Menu> General Postproc>List Results> Nodal Solution
Main Menu> General Postproc>List Results> Element Solution
Main Menu> General Postproc>List Results> Reaction Solution
В постпроцессоре POST1 предусмотрено много других функций, таких как масштабирование результатов в различные координатные системы, комбинация случаев нагружения и т. д
8.6 Пример расчета простой системы.
Описание задачи.
Балка с шарнирными опорами, длиной l, массой m, распределенной по длине, подвергается вертикальной вибрации на обеих опорах. Вибрация определена как спектр перемещений. Определить перемещения узлов, усилия реакции и решение для элементов.
Исходные данные.
Модуль упругости Е=30*106psi
Масса m=0.2 ibsec2/in2
Момент инерции поперечного сечения J=1000/3 in4
Площадь поперечного сечения A=273.9726 in2.
Длина балки l=240 in
Высота сечения h=14 in.
|
Спектр воздействия |
|
|
Частота, Гц |
Перемещение, in |
|
0.1 800 |
0.44 0.44 |
1. Utility Menu>File>Change Title
2. Введите текст «Seismic response of beam structure» и нажмите ОК.
Определение типов элементов
1. Main Menu>Preprocessor>Element Type>Add/Edit/Delete Откроется диалоговое меню.
2. Нажать на Add. Откроется диалоговое окно библиотеки элементов.
3. В левой части выбрать «Structural Beam»
4. В правой части нажать на « 2D elastic3».
5. Нажать ОК. Диалоговое окно элементов закроется.
6. Нажать на Close окна типов элементов.
Определение реальных констант.
1. Main Menu>Preprocessor>Real Constant. Откроется диалоговая коробка реальных констант.
2. Нажать Add. Откроется диалоговое окно типов элементов для реальных констант.
3. Нажать ОК. Откроется диалоговое окно для элемента BEAM3.
4. Введите 273.9726 как площадь поперечного сечения.
5. Введите (1000/3) для момента инерции.
6. Введите 14 для высоты балки.
7. Нажмите на Close.
Определение свойств материала.
1. Main Menu>Preprocessor>Material Props>Constant-Isotropic. Откроется диалоговое окно свойств материала.
2. Нажать на ОК, выбирая по умолчанию материал номер 1.Откроется диалоговое окно изотропных свойств материала.
3. Ввести 30e6 для модуля упругости.
4. Ввести 73E-05 для плотности нажать ОК.
Определение точек и линии.
1. Main Menu>Preprocessor>Modeling-Create>Keypoints> In Active Cs. Откроется диалоговое окно построения точек.
2. Введите 1 для номера точки.
3. Нажмите Apply выбирая по умолчанию координаты X,Y,Z равными нулю.
4. Введите 2 как номер точки.
5. Введите 240,0,0 для координат X,Y,Z .
6. Нажмите ОК.
7. Utility Menu>PlotCtrl>Numbering . Откроется диалоговая коробка нумерации.
8. Нажать на “keypoint numbering on»
9. Нажать ОК.
10. Main Menu>Preprocessor>Modeling-Create>Line> Straight Line. Откроется пиковое меню
11. Нажать на точку 1, затем на точку 2. Возникнет прямая линия между двумя точками.
12. Нажать ОК.
Установка разбиений.
1. Main Menu>Preprocessor>Meshing –Size Cntrls >Global – Size. Откроется диалоговое окно.
2. Введите 40, как число делений и нажмите ОК.
3. Main Menu>Preprocessor>Meshing –Mesh >Lines
4. Нажмите ALL.
Установка граничных условий.
1. Main Menu>Solutions>Loads-Apply >Structural-Displacement>On Nodes
2. В графическом окне нажать на узел на левом конце балки.
3. Нажать ОК.
4. Нажать на UY.
5. Нажать ОК.
6. Повторить шаги 1-3 и выбрать узел на правом конце балки.
7. В коробке нажать на UX и теперь и UX и UY будут выделены.
8. Нажать ОК.
Определение типа анализа и опции.
1. Main Menu>Solutions>Analys Type>New Analys
2. Выбрать “Modal» и нажать ОК. Откроется диалоговое окно.
3. Main Menu>Solutions>Analys Options Откроется диалоговое окно модального анализа.
4. Выбрать по умолчанию “Subspace» как метод раскрытия мод.
5. Введите 10 как число мод и нажмите ОК.
6. Нажмите на кнопку раскрытия мод [MXPAND] и выбрать «NO».
7. Нажмите ОК. Откроется диалоговое окно модального анализа.
8. Нажмите ОК.
Решение модального анализа.
1. Main Menu>Solution>Solve-Current LS
2. Просмотрите информацию в окне статуса нажмите Close.
3. Нажмите ОК на Solve Current Step.
4. Когда решение будет получено, возникнет сообщение «Solution is done”
Установка спектрального анализа.
1. Main Menu>Solutions>Analys Type>New Analys
2. Откроется диалоговая коробка с предупрежающей надписью “Изменение типа анализа правильно только внутри первого временного шага” Нажать ОК. Нажать на CLOSE.
3. Нажать на «Spectrum» и нажать ОК.
4. Выбрать по умолчанию единственный спектр реакции (SPRS) и ввести 10 для числа мод в решении.
5. Нажать на диалоговую кнопку, выбирая YES для расчета напряжений. Нажать ОК.
6. Main Menu>Solutions>Load Step Opt-Spectrum>Single-point-Settings. Откроется диалоговое окно.
7. Выбрать «Seismic displac”.
8. Введите 0,1,0 для выбора направления воздействия.
Определение величины спектра из таблицы частот.
1. Main Menu>Solutions>Load Step Opt-Spectrum>Single-Point-Freq Table.
2. Введите 0.1 для FREQ1 и 800 для FREQ2 и нажмите ОК.
3. Main Menu>Solutions>Load Step Opt-Spectrum>Single-Point-Spectr Values. Откроется диалоговое окно Значение спектра - Отношение демпфирования.
4. Нажмите ОК, выбирая по умолчанию без демпфирования. Откроется диалоговая коробка значения спектра.
5. Введите 0.44 и 0.44 для FREQ1 и FREQ2.
6. Нажмите ОК.
Решение спектрального анализа.
1. Main Menu>Solution>Solve-Current LS
2. Просмотрите информацию в окне статуса нажмите Close.
3. Нажмите ОК на Solve Current Step.
4. Когда решение будет получено, возникнет сообщение «Solution is done”
Установка шага расширения мод.
1. Main Menu>Solutions>Analys Type>New Analys
Откроется диалоговая коробка с предупрежающей надписью “Изменение типа анализа правильно только внутри первого временного шага” Нажать ОК. Нажать на CLOSE.
2. Нажать на «Modal» и нажать ОК.
3. Main Menu>Solutions>Expansion Pass
4. Нажать на диалоговую кнопку в положение ON и нажать ОК.
Раскрытие мод.
1. Main Menu>Solution>Load Step Opts-Expansion Pass>Single Expand-Expan Modes.
2. Введите 10 для числа мод и введите 0.005 для порога важности.
3. Нажмите на кнопку результатов элементов, выбирая YES.
4. Нажмите ОК.
Выполнение раскрытия мод.
1. Main Menu>Solution>Solve-Current LS
2. Просмотрите информацию в окне статуса и нажмите Close.
3. Нажмите ОК.
4. Когда решение будет получено, возникнет сообщение «Solution is done”
Установка комбинирования мод для спектрального анализа.
1. Откроется диалоговая коробка с предупрежающей надписью “Изменение типа анализа правильно только внутри первого временного шага” Нажать ОК. Нажать на CLOSE.
2. Нажать на Spectrum и нажать ОК.
3. Main Menu>Solutions>Analys Options. Откроется диалоговое окно спектрального анализа.
4. Выбрать по умолчанию единственный спектр реакции (SPRS). Нажать ОК.
Выбор метода раскрытия мод.
1. Main Menu>Solutions>Load Step Opt-Spectrum>Single-Mode Combine. Откроется диалоговое окно.
2. Выбрать SRSS как метод комбинирования мод.
3. Ввести 0.15 как порог важности.
4. Выбрать перемещения как тип выходных данных. Нажать ОК.
Комбинирование мод
1. Main Menu>Solution>Solve-Current LS
2. Просмотрите информацию в окне статуса и нажмите Close.
3. Нажмите ОК.
4. Когда решение будет получено, возникнет сообщение «Solution is done”
Постпроцессор: вывод на печать узловых и элементных данных, реакций.
1. Main Menu> General Postproc>List Results> Results Summary. Откроется окно листинга.
2. Просмотрите информацию и нажмите Close.
3. Utility Menu>File>Read Input From. Откроется диалоговое меню чтения файлов.
4. В левой части диалогового окна выбрать директорию, содержащую ваши результаты.
5. В правой части окна выбрать файл Jobname.mcom.
6. Нажать ОК.
7. Main Menu> General Postproc>List Results> Nodal Solution.
8. В левой части диалогового окна выбрать по умолчанию DOF solution, а в правой части «All DOFs DOF»
9. Откроется окно листинга. После просмотра нажать Close.
10. Main Menu> General Postproc>List Results> Element Solution. Откроется диалоговое окно решения элементов.
11. В левой части диалогового окна выбрать «Line Elem Result» и выбрать «Structural ELEM» в правой части. Нажать ОК.
12. Откроется листинг. После просмотра нажать Close.
13. Main Menu> General Postproc>List Results> Reaction Solution.
14. В левой части меню выбрать «All struc fors F» и нажать ОК.
15. Откроется листинг. После просмотра нажать Close.
8.7 Как выполнить анализ случайных колебаний.
Процедура анализа случайных колебаний состоит из шести основных шагов:
1. Построение модели;
2. Получение модального решения;
3. Раскрытия мод;
4. Получение спектрального решения;
5. Комбинирование мод;
6. Просмотр результатов.
Первые два шага – те же самые, что для спектрального анализа. Анализ случайных колебаний не предусмотрен для программы ANSYS/Linear Plus.
При использовании интерфейса, в диалоговом окне модального анализа [MODOPT] содержатся опции для раскрытия мод [MXPAND]. Нажмите «YES» для раскрытия мод. Здесь процедура получения модального анализа и раскрытия мод объединена в один шаг.
8.7.1 Раскрытие мод.
Вы должны раскрыть моды, полученные методом подпространства, блочным методом и редуцированным методом. При этом необходимо учесть некоторые особенности:
Только раскрытые моды учитываются в шаге комбинирования мод;
Если вас интересует вычисление напряжений, возникающих от действия спектра, их нужно «заказать» здесь.
Раскрытие мод может быть отдельным шагом решения, или может быть включено в модальный анализ.
В конце шага раскрытия мод выйдите из режима «решение» командой FINISH.
8.7.2.Получение спектрального решения
Для получения спектрального решения база данных должна содержать данные модели и следующие файлы из модального анализа: Jobname.MODE,.ESAV,.EMAT,.FULL,.RST и DB.
1. Войдите в решение.
Main Menu>Solutions.
2. Определите тип анализа и опции.
Для типа спектра [SPOPT] выберите спектральную плотность мощности (PSD);
Выберите расчет напряжений (ON), если это вас интересует.
3. выберите опции шагов нагрузки. Возможны следующие опции:
Spectrum Data
Тип спектральной плотности.
Спектральная плотность может быть задана в виде перемещения, скорости, силы, давления, ускорения. Это будет или возбуждение основания, или возбуждения узлов в шагах 4и 5. Если применяется спектральная плотность в виде давления, то давление должно быть определено в модальном анализе.
Команда: PSDUNIT.
Main Menu>Solution>Spectrum>-PSD-Setting.
Таблица спектральной плотности в функции частоты.
Команды: PSDFRQ, PSDVAL.
Интерфейс: Main Menu>Solution>Spectrum>-PSD-PSD vs Freq.
В шаге 6 описано, как применить дополнительное возбуждение от спектральной плотности.
Демпфирование (динамические опции).
Возможны следующие формы демпфирования ALPHAD, BETAD, MDAMP.
Альфа, демпфирование, пропорциональное матрице масс.
Команда ALPHAD.
Main Menu > Solution> Load Step Opts-Time/Frequenc>Damping.
Бета демпфирование, пропорциональное матрице жесткости.
Команда BETAD.
Main Menu > Solution> Load Step Opts-Time/Frequenc>Damping.
Постоянное отношение демпфирования.
Команда DMPRAT.
Main Menu > Solution> Load Step Opts-Time/Frequenc>Damping.
Частотно-зависимое отношение демпфирования.
Команда MDAMP.
Main Menu > Solution> Load Step Opts-Time/Frequenc>Damping.
4. Приложите возбуждение от спектральной плотности мощности к выбранным узлам. Используйте значение 1.0 для обозначения точек, где прикладывается возбуждение. Значение 0.0 может использоваться для удаления спецификации. Направление возбуждения выбирается с помощью меток UX, UY, UZ команды D (при возбуждении основания) и меток FX, FY, FZ команды F при возбуждении узлов. При возбуждении узлов значение, больше, чем 1.0 может быть использовано для масштабного фактора участия. Для спектральной плотности в виде давления необходимо перенести вектор нагрузки из модального анализа [LVSCALE]. Вы можете приложить возбуждение основания только в тех узлах, что были закреплены в модальном анализе.
Команды D или DK, DL, DA для возбуждения основания.
F или FK для возбуждения узлов. LVSCALE для давления.
Интерфейс: Main Menu>Solution>-Loads-Apply>Spectrum>-BasePSD Excit-On Nodes.
5. Рассчитайте фактор участия для возбуждения спектральной плотностью. Используйте поле TBLNO (номер таблицы) какая именно таблица спектральной плотности будет применяться и поле Ecxit для для обозначения, будет ли возбуждаться основание или узел.
Команда PFACT.
Интерфейс: Main Menu>Solution>-Load Step Opts - Spectrum>-PSD- Calculate PF
6. Если вам необходимо приложить несколько воздействий в виде спектральных плотностей к одной и той же модели, повторите шаги 3, 4, 5 для каждой дополнительной спектральной плотности. Затем определите, если это необходимо степень корреляции между возбуждениями, используя следующие команды:
COVAL для взаимной спектральной плотности;
QDVAL для квадратичных спектральных значений;
PSDSPL для пространственных соотношений;
PSDWAV для соотношений при распространении волны.
Интерфейс: Main Menu>Solution>-Load Step Opts - Spectrum>-PSD- Correlation
Когда вы используете команды PSDSPL или PSDWAV вы должны соответственно использовать SPATIAL или WAVE в команде PFACT.
7. Выбор управления выходными параметрами.
Только команда PSDRES обеспечивает правильный контроль выходных данных и запись результирующего файла. Может быть выполнено три вида расчета: перемещение, скорость, ускорение. Каждое из них может быть определено относительно основания или абсолютно.
Команда PSDRES.
Интерфейс: Main Menu>Solution>-Load Step Opts - Spectrum>-PSD- Calc Controls.
В таблице 8.3 приведены возможные настройки решения.
Таблица 8.3
|
Решение |
Параметры |
Форма |
|
Перемещения (метка DISP в команде PSDRES) |
Перемещения, напряжения, деформации, силы |
Относительное, абсолютное, или оба |
|
Скорость (метка VELO в команде PSDRES) |
Скорость, скорость напряжения, и т. д. |
Относительное, абсолютное, или оба |
|
Ускорение (метка ACEL в команде PSDRES) |
Ускорение, ускорение напряжения и т. д. |
Относительное, абсолютное, или оба |
Main Menu>Solution>Solve-Current LS.
9. Выйдите из режима решения.
8.7.3 Комбинирование мод.
1. Войдите в решение.
Main Menu>Solutions.
2. Определите тип анализа.
Опция NEW Analysis [ANTYPE]
Выберите тип анализа - spectrum.
3. Только PSD mode combination метод является допустимым для анализа случайных колебаний. Этот метод позволяет рассчитывать перемещения в форме одной сигмы, напряжения и т. д. в модели. Если вы не введете команду PSDCOM, программа не будет считать параметры в виде одной сигмы.
Команда PSDCOM
Интерфейс: Main Menu>Solution>-Load Step Opts - Spectrum>-PSD- Mode Combin.
Поля SIGNIF и COMODE часто используются для снижения числа мод. Если вы хотите испробовать эту опцию необходимо распечатать модальную ковариационную матрицу для начального получения относительной комбинации мод.
4. Запустите решение.
Main Menu>Solution>Solve-Current LS.
5.Выйдите из режима решения.
8.7.4 Просмотр результатов.
Результаты анализа случайных колебаний записываются в результирующий файл Jobname.RST. Они состоят из следующих данных:
1. Раскрытые формы мод из модального анализа.
2. Статическое решение при возбуждении основания. [PFACT,,BASE].
3. Следующие данные, если на этапе комбинации мод введена команда [PSDCOM] и сделаны установки команды [PSDRES].
1s перемещение (напряжения, деформации, силы);
1s скорость и т. д.
1s ускорение и т. д.
Вы можете просмотреть эти результаты в постпроцессоре POST1, затем рассчитать выходную спектральную плотность в постпроцессоре POST 26.
Для просмотра результатов в POST1 вы сначала должны понять, как эти данные организованы в результирующем файле. Организация файла приведена в таблице 8.4.
Таблица 8.4
|
Шаг нагрузки |
Подшаг |
Комментарии |
|
1 |
1 2 3 |
Раскрытая мода 1 Раскрытая мода 2 Раскрытая мода 3 |
|
2 Возбуждение основания |
1 2 3 |
Единичное статическое решение для таблицы СПМ 1 Единичное статическое решение для таблицы СПМ 2 |
|
3 |
1 |
1 сигма перемещение |
|
4 |
1 |
1 сигма скорость |
|
5 |
1 |
1 сигма ускорение |
1. Прочитайте набор результатов в базу данных. Например, для чтения 1s перемещения введите команду SET,3,1.
Интерфейс: Main Menu>General Postproc>-Read Results-First Set
2. Можно использовать те же опции, что для спектрального анализа.
Примечание: Осреднение напряжений в узлах с помощью команды PLNSOL может не соответствовать при анализе случайных колебаний, потому что напряжения здесь понимаются в статистическом смысле.
8.7.5 Расчет выходной спектральной плотности в POST26.
Вы можете рассчитать и нарисовать выходную спектральную плотность перемещения, скорости или ускорения, если получены файлы Jobname.RST и Jobname.PSD.
1. Войдите в постпроцессор POST26.
Команда /POST26
Интерфейс: Main Menu>TimeHist PostPro
2. Подготовьте вектор частот. NPTS –число точек на частотной оси, добавляемых по обе стороны от собственной частоты для получения плавной кривой. (По умолчанию –5). Вектор частот принимается как переменная номер 1.
Команда STORE, PSD,NPTS
Интерфейс: Main Menu>TimeHist PostPro>Store Data.
3. Определите переменные (перемещения, напряжения и т. д. ).
Команды NSOL, ESOL.
Интерфейс: Main Menu>TimeHist PostPro>Define Variables.
4. Расчет выходной спектральной плотности и сохранение его в выбранных переменных.
Команда RPSD.
Интерфейс: Main Menu>TimeHist PostPro>Calc Resp PSD.
8.7.6 Вычисление ковариационных функций в POST26
Вы можете вычислить ковариацию между двумя переменными, записанными в результирующий файл (перемещениями, скоростями, ускорениями), если имеются файлы Jobname.RST и Jobname.PSD.
1. Войдите в постпроцессор POST26.
Команда /POST26
Интерфейс: Main Menu>TimeHist PostPro
2. Определите переменные, в которых содержатся интересные для вас данные.
Main Menu>TimeHist PostPro>Define Variables.
3. Рассчитайте вклад каждой компоненты (относительно абсолютной реакции) и сохраните их в выбранной переменной. Команда PLVAR может быть использована для рисования модальных вкладов (относительно реакции), псевдостатической и смешанной части в ковариационной функции.
Команда CVAR.
Main Menu>TimeHist PostPro>Calc Covarince.
4. Получение ковариаций.
Команда *GET,NameVAR1,n,EXTREM,CVAR.
Интерфейс: Utility Menu>Parameters>Get Scalar Data
8.8 Как выполнить анализ множественного спектра реакции.
Процедура для определения множественного спектра реакции та же самая, что для случайной вибрации со следующими отличиями:
Выберите MPRS вместо PSD как тип спектра в команде [SPOPT];
Таблица спектральной плотности в функции частоты представлена как таблица спектральных значений в функции частоты;
Вы можете выбрать некоторую степень корреляции между спектрами, или считать их некоррелированными;
Определяются только относительные результаты (относительно возбуждения основания), абсолютные значения не определяются.
Поддерживаются все методы комбинирования мод, за исключением PSDCOM.
Результаты анализа множественного спектрального анализа записываются в файл Jobname.MCOM в форме команд постпроцессора POST1. Предусмотрены команды расчета предельных реакций системы комбинацией максимальных модальных реакций. Предельные реакции состоят из предельных перемещений, предельных напряжений, предельных деформаций и сил реакции.
Часть 2. Основы теории.
9. МОДАЛЬНЫЙ АНАЛИЗ
Модальный анализ используется для определения собственных частот и форм колебаний конструкции. Предполагается, что совершаются свободные незатухающие колебания:

Отметим, что матрица жесткости конструкции [K] может включать в себя эффект предварительного нагружения.
Для линейной системы свободные колебания будут гармоническими:

где


t - время.
Таким образом, матричное уравнение (9.1) принимает следующий вид:

Это уравнение имеет решение, кроме тривиального



Последнее уравнение и есть задача о собственных значениях. Решением уравнения (4), если n - порядок матрицы, является характеристический полином n-го порядка, который имеет n корней:



- число степеней свободы. Эти корни являются собственными значениями уравнения. Собственные вектора





Значения собственных круговых частот


где

Обычно собственный вектор


то есть

В другом случае собственный вектор

При использовании метода частотной конденсации (редукции степеней свободы) n
собственных векторов затем могут быть развернуты на этапе “расширения” до полного набора модальных степеней свободы конструкции:

где



10. МЕТОД СУПЕРПОЗИЦИИ МОД
Метод суперпозиции мод использует данные о собственных частотах и формах колебаний, полученные путем проведения модального анализа, для оценки динамического отклика конструкции от нестационарных или стационарных гармонических возмущений.
Уравнения движения могут быть выражены в следующей форме:

где [M] - матрица масс системы;
[C] - матрица демпфирования системы;
[K] - матрица жесткости системы;
{u''} - вектор узловых ускорений;
{u'} - вектор узловых скоростей;
{u} - вектор узловых перемещений;
{F} - вектор прикладываемых сил, переменных во времени, который можно расписать как:
{F} = {Fnd} + s{Fs} (10.2)
где {Fnd} - вектор переменных во времени узловых силы;
s - масштабный коэффициент вектора нагрузок;
{Fs} - вектор нагрузок, полученный путем модального анализа (см. далее).
Вектор нагрузки {Fs} вычислен при выполнении анализа форм колебаний. Он образуется точно так же как и вектор нагрузки подконструкции .
Следующая разработка подобна данной в книге Бате [2].
Определим набор модальных координат yi из условия, чтобы

где

n - число используемых мод (вводится с помощью команд TRNOPT или HROPT).
Заметьте, что уравнение (10.3) препятствует использованию отличного от нуля входного перемещения, после определения yi не напрямую, а через {u}. Обратная зависимость существует (уравнение (10.3)) для случая, где все смещения известны, но не, когда только некоторые известны. Подставив уравнение (10.3) в (10.1) получим:

Умножая слева на типичную форму колебаний


Из условия ортогональности собственных форм колебаний следует, что

В методе суперпозиции мод, разрешено только релеевское или постоянное демпфирование вследствие того, что

Применяя эти условия к уравнению (10.5) останутся только члены при


Коэффициенты



А. Коэффициент

При условии нормирования (17.3-6) -


В. Коэффициент

Член демпфирования основан на обработке модальных координат, как отдельных систем с одной степенью свободы (то есть независимых уравнений 15.11-1) для которой

и
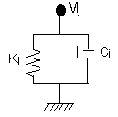 |

Рисунок 10.1 - Осциллятор с одной степенью свободы
Из уравнения (10.12) можно определить


Из Тси (68)

где

и

где

Объединение уравнения (10.13) с уравнениями (10.15) и (10.11)

С. Коэффициент yj
Из уравнения (10.3), то есть из


Перемножим слева на


Подставим уравнение (10.10) для масс -


Введем условное обозначение, пусть

представляет правую часть уравнения (10.9). Подставим уравнения (10.10), (10.16), (10.19) и (10.20) в уравнение (10.9), и получим уравнение движения для модальных координат:

Поскольку j представляет любую моду, уравнение (10.21) представляет n независимых друг от друга уравнений для n неизвестных yj. Преимущество разъединенной системы состоит в том, что вся в вычислительном отношении дорогая матричная алгебра была сделана в собственном решающем устройстве, и длинные переходные режимы могут быть проанализированы недорого в главных координатах с помощью уравнения (10.21). В гармоническом анализе, частоты могут быть отсканированы быстрее, чем методом редуцированного гармонического отклика. Значения yi
преобразуется назад в геометрические перемещения {u} (отклик системы на нагрузку), используя уравнение (10.3). То есть отдельные модальные отклики yi
накладываются друг на друга, чтобы получить фактический отклик, отсюда название "суперпозиция мод". Если анализ форм колебаний был выполнен, используя метод конденсации (MODOPT, REDUC), то матрицы и векторы нагрузки в вышеупомянутых уравнениях будут содержать главные (удерживаемые) степени свободы (то есть {u}).
10.1 Модальное демпфирование
Модальное демпфирование,


где a - множитель инерционного демпфирования (вводится командой ALPHAD)
b - множитель конструкционного демпфирования (вводится командой BETAD)
x - коэффициент постоянного демпфирования (вводится командой DMPRAT)
xmj - коэффициент модального демпфирования (вводится командой MDAMP)
Из-за предположения в уравнении (10.8), явное демпфирование в таких элементах как COMBIN14 не позволяется процедурой суперпозиции форм колебаний.
11. СПЕКТРАЛЬНЫЙ АНАЛИЗ
Поддерживаются два типа спектрального анализа: детерминированный метод спектрального отклика и недетерминированный метод случайных колебаний. Допускается возбуждение в опорах (например, сейсмическое воздействие) и возбуждение в точках, удаленных от опор. Существуют четыре вида спектрального анализа:
однофакторный спектральный анализ;
многофакторный спектральный анализ;
расчетно-экспериментальный метод динамического анализа;
метод спектральной плотности мощности.
Однофакторный спектральный анализ предполагает использование одной и той же спектральной кривой (например, зависимости изменения силы от времени) для всех возбуждаемых точек.
Многофакторный спектральный анализ предполагает задание в точках возбуждения различных спектральных кривых.
Расчетно-экспериментальный метод динамического анализа используется для оценки прочности корабельного оборудования. Метод состоит в получении отклика системы на спектр, который получен на основе эмпирических уравнений и таблиц расчета на удар, представленных в отчете NRL-1369 Лаборатории научных исследований военно-морских сил США.
Метод спектральной плотности мощности
представляет собой вероятностный подход к нахождению спектрального отклика и известен как анализ случайных колебаний.
11.1 Допущения и ограничения
1. Конструкция является линейной.
2. Для однофакторного спектрального анализа и расчетно-экспериментального метода динамического анализа возмущение на конструкцию задается спектром с известным направлением и частотными составляющими, воздействующими равномерно на все опорные точки или на заданные удерживаемые (главные) не опорные степени свободы (при использовании метода частотной конденсации).
3. Для многофакторного спектрального и спектральной плотности мощности видов анализа, конструкция может возмущаться различными входными спектрами с приложением их к различным опорным точкам и не опорным (свободным от связей) узлам. Можно задавать до десяти различных входных спектров.
11.2 Описание анализа
Спектральный анализ возможен при выборе типа анализа (ANTYPE, SPECTR) и если предварительно был выполнен модальный анализ. Если нужно объединение мод, то требуемые моды могут быть получены путем "расширения" (восстановления), как описано в разделе 17.3 (при применении метода частотной конденсации).
Поддерживаются четыре опции - однофакторный спектральный анализ (SPOPT, SPRS), расчетно-экспериментальный метод динамического анализа (SPOPT, DDAM), метод спектральной плотности мощности (SPOPT, PSD) и многофакторный спектральный анализ (SPOPT, MPRS). Каждая опция подробно описывается далее.
11.3 Однофакторный спектральный анализ (SPOPT, SPRS)
Поддерживаются два вида возмущений: заданное на опоры (кинематическое возмущение, например, сейсмическое) и в зонах удаленных от опор (силовое возмущение). Все требуемые данные смотри в таблице 11.1
