Типы спектральной нагрузки
| Опции возмущений | |||||
| Опорное возмущение | Возмущение удаленное от опор | ||||
| Спектр на входе | Таблица, характеризующая спектр (команды FREQ и SV) | Таблица множителей амплитуды
(команды FREQ и SV) | |||
| Ориентация нагрузки | Направляющий вектор, вводимый командой SED | Направления X, Y и Z, выбранные как опции FX, FY, FZ команды F | |||
| Распределение нагрузок | Равномерное на все опорные точки | Амплитуда в направлении X, Y, Z выбирается как VALUE команды F | |||
| Тип входа | Скорость, Ускорение, Перемещение | Сила | |||
| KSV из команды SVTYP | 0 2 3,4 | 1 |
Демпфирование
Демпфирование учитывается для каждой моды и определяется как:

где









Заметьте, что зависящий от материала вклад демпфирования вычисляется на этапе "расширения" (восстановления) мод, так, чтобы этот вклад от демпфирования был туда включен.
11.3 Коэффициенты вклада и модальные коэффициенты
Коэффициенты вклада для заданного направления возмущения определяется как:


где





Вектор, определяющий направление возмущения имеет форму:

где


1. Для значения D основанного на команде SED:



где Sx , Sy , Sz - входные значения SEDX, SEDY и SEDZ, соответственно для команды SED

2. Для значения D основанного на командах SED и ROCK:



R определяется как:

где Сx , Сy , Сz - входные значения OMX, OMY и OMZ, соответственно в команде ROCK;

rx = Xn
- Lx
ry = Xn
- Ly
rz = Xn
- Lz
Xn, Yn, Zn - координаты узла n
Lx , Ly , Lz - положение центра вращения (входные значения CGX, CGY и CGZ в команде ROCK).
Вектор перемещений, скорости и ускорения для каждой моды вычисляется из собственного вектора с помощью "модального коэффициента":

где

метка - три поля в командах объединения мод (SRSS, CQC, GRP, DSUM, NRLSUM);

Ai - модальный коэффициент (см. далее).
Модальный коэффициент вычисляется в пяти различных направлениях, в зависимости от типа возмущения (команда SVTYP).
1. Для SVTYP, 0 (возмущение прикладывается к опоре в виде скорости):

где Svi - спектральная скорость для i-ой моды (найденная из входного спектра скорости на частоте fi и эффективном коэффициенте демпфирования

fi - i-ая собственная частота ( число циклов за единицу времени = wi/2p);
wi - i-ая собственная круговая частота (радиан за единицу времени).
2. Для SVTYP, 1 (возмущение прикладывается в виде силы):

где Sfi - спектральная сила для i-ой моды (находится из входной таблицы множителей амплитуды на частоте fi и эффективном коэффициенте демпфирования

3. Для SVTYP, 2 (возмущение прикладывается к опоре в виде ускорения):

где Sai - спектральное ускорение для i-ой моды (найденное из входного спектра ускорения на частоте fi и эффективном коэффициенте демпфирования

4. Для SVTYP, 3 (возмущение прикладывается к опоре в виде перемещения):

где Sui - спектральное перемещение для i-ой моды (найденное из входного спектра перемещений на частоте fi и эффективном коэффициенте демпфирования

5. Для SVTYP, 4 (спектральная плотность мощности (СПМ), читай Ванмарке (34) в списке литературы теоретического руководства)

где Spi - спектральная плотность мощности для i-ой моды (получена из входной спектральной плотности на частоте fi и эффективном коэффициенте демпфирования


Интеграл в вышеупомянутом уравнении аппроксимируется как:

где Li = fi (в целочисленной форме);
Spj - спектральная плотность мощности оцененная на частоте (f) равной j (в вещественной форме);
Df - эффективная полоса частот для fi = 1.
Когда Svi, Sfi, Sai, Sui, или Spi требуется между табличными значениями входных частот, выполняется логарифмическая интерполяция.
Спектральные значения и модальные коэффициенты выводятся в таблицу "RESPONSE SPECTRUM CALCULATION SUMMARY" заданной входной кривой с наименьшим коэффициентом демпфирования, без эффективного коэффициента демпфирования.
12. АНАЛИЗ СЛУЧАЙНЫХ КОЛЕБАНИЙ
Метод позволяет прикладывать несколько возмущений в виде спектральных плотностей мощности (PSD) на входы системы (до десяти), которые могут быть:
1. Полностью коррелированные,
2. Некоррелированные, или
3. Частично коррелированные.
Процедура основана на статистических вычислениях каждого модального отклика, и затем их объединении (суммировании или комбинировании). Принимается, что возбуждения – стационарные случайные процессы.
12.1 Описание метода
Для частично коррелированных силовых и кинематических возмущений, полные уравнения динамического поведения конструкции разделяются на две части для неизвестных и заданных перемещений соответственно:

где {uf} - вектор неизвестных перемещений (от силовых возмущений);
{ur} - вектор заданных перемещений (возбуждаемых случайной нагрузкой, задается единичное перемещение);
{F} - заданное силовое возмущение (значение силы может быть отличным от единицы, при учете масштабирования от коэффициентов вклада);
{0} - вектор сил реакции, соответствующая вектору заданных перемещений {ur}.
Неизвестные перемещения могут быть расчленены на псевдо-статические и динамические части:
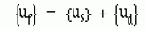
Псевдо-статические перемещения могут быть получены из уравнения (12.1) исключением первых двух слагаемых в левой части уравнения и, заменой вектора неизвестных перемещений {uf} на вектор их псевдо-статических составляющих {us}
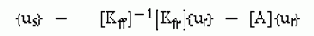
где

Элементы по i-ому столбцу [A] представляют собой псевдо-статические перемещения от единичных заданных перемещений возбужденных i-ой спектральной плотностью мощности (PSD). Подставим уравнения (12.3) и (12.2) в (12.1) и добавим незначительное демпфирование. Первая строка матричного уравнения (12.1) тогда может быть переписана в следующем виде:
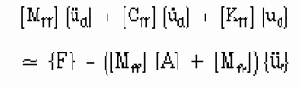
Второе слагаемое в правой части вышеупомянутого уравнения представляет эквивалентные силы, обусловленные кинематическими возмущениями.
При использовании метода суперпозиции мод уравнения (10.3) запишутся вновь как:
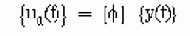
Вышеупомянутые уравнения несвязанны друг с другом и запишутся как n отдельных уравнений:
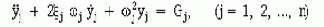
где n - число форм колебаний, выбранных для оценки;
yj
- обобщенные перемещения;
wj и xj - собственные круговые частоты и модальные коэффициенты демпфирования.
Модальные нагрузки Gj определяются как:
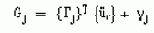
Модальные коэффициенты вклада (участия) соответствующие кинематическим возмущениям даются как:
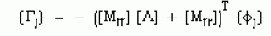
и для силового возмущения
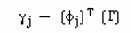
Формы колебаний {fj} должны быть нормированы относительно матрицы масс как в уравнении (9.6):
{f}jT[M]{f}j = {I}.
12.2 Спектральные плотности мощности отклика и среднеквадратичное значение отклика
Используя теорию случайных колебаний, отклик в виде спектральных плотностей мощности может быть вычислен от входных СПМ с помощью передаточной функцией для одной степени свободы системы Н(w), используя метод суперпозиции мод. Отклик спектральной плотности мощности, для i-ой степени свободы дается как:
Динамическая часть
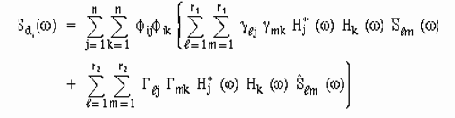
Псевдо-статическая часть
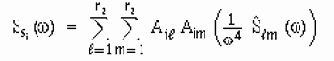
Ковариационная часть
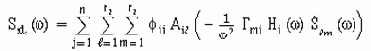
где n - число форм колебаний, выбранных для оценки;
r1
и r2 - число силовых (удаленных от опор) и кинематических СПМ-таблиц, соответственно.
Передаточные функции типа для системы с одной степенью свободы принимают различные формы в зависимости от типа вводимой СПМ и типа желательного отклика. Формы передаточных функций для перемещения как выхода перечислены ниже для различных случаев.
1. На входе - сила или ускорение:
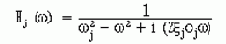
2. На входе - перемещение
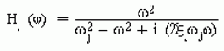
3. На входе - скорость
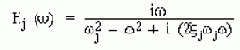
где w - частота возбуждения
wj
– собственная круговая частота j-ой моды
i = Ö-1 – мнимая единица.
Таким образом, анализ случайных колебаний может использоваться, чтобы показать абсолютное среднеквадратичное значение отклика неизвестных перемещений:
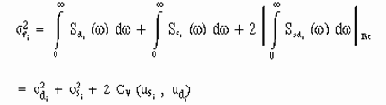
где | |Re – обозначает вещественную часть аргумента;


перемещениями
Общая формулировка, описанная выше, дает упрощенные уравнения для некоторых ситуаций, с которыми обычно приходится сталкиваться на практике. Для полностью коррелированных силовых возмущений и идентичных заданных перемещений, нижние индексы l и m исключали бы уравнения с (12.10) до (12.12). Когда существуют только силовые возмущения, последние два члена в уравнении (12.16) не применяют, и только первый член в пределах больших круглых скобок в уравнении (12.10) обязательно будет учитываться. Для некоррелированных силовых и кинематических возмущений, взаимные спектральные плотности мощности (то есть когда l ¹ m) равны нулю, и только члены, для которых l = m в уравнениях (12.10) через (12.12) обязательно будут учтены.
Уравнения (12.10) до (12.12) могут быть перезаписаны как:



где

Решение в закрытой форме получено для кусочно-линейной СПМ (PSD) в логарифмическом масштабе по обеим осям, применявшимися для вычисления каждого интеграла в уравнении (12.16) (Чен и Али (193), и Харичандран (194)). Впоследствии, дисперсия становится:
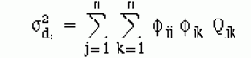
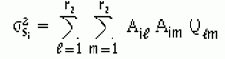
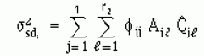
Модальные матрицы ковариации



Дисперсия для напряжений, узловых сил или реакций может быть вычислена из уравнений, подобных с (12.20) по (12.22). Если желательно получить дисперсию напряжения, замените формы колебаний (fij) и статические перемещения (







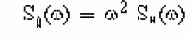

12.3 Не диагональные спектральные члены для частично коррелированных входных спектральных плотностей мощности
Для возмущений определяемых более, чем одной функцией спектральной плотности мощности (СПМ), перекрестные члены которые определяют степень корреляции между различными функциями СПМ определяют как:

где



Взаимная функция спектральной плотности мощности (СПМ) называется функцией когерентности:

где

Хотя вышеупомянутый пример демонстрирует взаимную корреляцию для 3 входных спектров, эта матрица может иметь диапазон в размере от 2 x 2 до 10 x 10 (то есть, максимальное число таблиц - 10).
Для частного случая, в котором все перекрестные члены являются нулевыми, входные спектры, как считают, некоррелированны. Заметим, что корреляция между силовыми и кинематическими возмущениями не позволяется.
12.4 Корреляционное пространство
Степень корреляционной связи между возбужденными узлами может также задаваться. В зависимости от расстояния между возбужденными узлами и значениями RMIN и RMAX, воздействие от спектральной плотности мощности может быть задано таким, что возбуждение в узлах может быть некоррелированно, частично коррелированно или полностью коррелированно. Если расстояние между возбужденными узлами - меньше чем RMIN, то эти два узла полностью коррелированные; если расстояние большее чем RMAX, то эти два узла некоррелированные; если расстояние находится между RMIN и RMAX, возбуждение частично коррелированно и основано на фактическом расстоянии между узлами. Рисунок ниже указывает, как соотносятся RMIN, RMAX и корреляционная связь.
Для двух возбужденных точек 1 и 2, спектральная плотность мощности была бы:

где:

D12 - расстояние между двумя возбуждаемыми точками 1 и 2;
So(w) - заданная на вход СПМ.
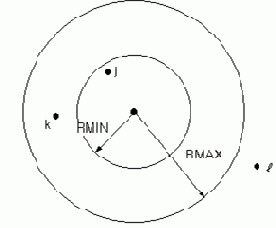
Рисунок 12.1 Сферы влияния, отражающие пространство корреляции возмущений заданных спектральной плотностью мощности
Возбуждение узла i полностью коррелированно с возбуждением узла j.
Возбуждение узла i частично коррелированно с возбуждением узла k
Возбуждение узла i некоррелированно с возбуждением узла l.
12.5 Распространение волн
Чтобы включать эффекты распространения волн по конструкции от случайного нагружения, возмущение PSD задано как:

где:


V- Скорость распространения волны по осям X, Y и Z.

Допускается более чем одна одновременная волна или пространственно коррелированные входные спектральные плотности мощности, когда входное воздействие [S(w)] отражает влияние двух или более некоррелированных входных спектров. В этом случае, частичная корреляция среди заданных на входы системы спектральных плотностей мощности в настоящее время не разрешается.
12.6 Метод многофакторного спектрального анализа (SPOPT, PSD)
Анализ спектрального отклика поддерживает многофакторные кинематические и силовые возмущения, разрешая до 10-ти различных спектральных таблиц которые могут быть не связаны (некоррелированны) между собой.
Много составляющих для выполнения анализа многофакторного спектрального отклика системы уже рассмотрены в предыдущих подразделах, посвященных методу случайных вибраций. Полагая, что коэффициенты вклада


где

Модальные коэффициенты объединяются с использованием метода квадратного корня из суммы квадратов (SRSS):

Формы колебаний, модальные напряжения и другие результаты, после умножения на модальные коэффициенты, затем могут быть объединены с помощью любого из доступных способов объединения мод: (квадратного корня из суммы квадратов (SRSS), полного квадратичного объединения (CQC), двойной суммы (DSUM), группирования (GRP) или методом суммирования (DDAM) Лаборатории (NRL) военно-морских сил США), как описано в предыдущих разделах, посвященных однофакторному спектральному анализу.
Содержание
1. Порядок работы в ANSYS ………………………………………………………………………3
1.1 Построение модели………………………………………………………………………………3
1.2 Определение типов элементов………………………………………………………………….3
1.3 Задание реальных констант элементов…………………………………………………………4
1.4 Использование процедуры определения поперечных сечений………………………………5
1.5 Определение свойств материалов………………………………………………………………5
1.6 Использование файлов библиотеки материалов………………………………………………6
1.7 Нелинейные свойства материала……………………………………………………………….7
2. Создание модели (предварительные замечания)………………………………………………7
2.1 Планирование работы……………………………………………………………………………8
2.2 Определение объекта…………………………………………………………………………….8
2. 3 Выбор между линейными элементами и элементами высокого порядка……………………9
2.4 Линейные элементы без узлов на срединах сторон…………………………………………. .10
2.5 Квадратичные элементы с узлами в срединах сторон……………………………………….. 11
2.6 Ограничения, на соединения элементов различных типов………………………………….. 14
2.7 Использование преимуществ симметрии…………………………………………………….. 15
2.8 Некоторые рекомендации по осесимметричным системам………………………………… .15
3. Системы координат……………………………………………………………………………… 17
4. Рабочее поле………………………………………………………………………………………19
5. Сравнение методов твердотельного моделирования и непосредственной генерации……….20
6. Построение твердотельной модели «снизу вверх» ……………………………………………23
6.1 Точки……………………………………………………………………………………………..23
6.1.1 «Тяжелые» (Hard) точки…………………………………………………………………… 24
6.2 Линии…………………………………………………………………………………………….26
6.3 Поверхности…………………………………………………………………………………… 28
6.4 Объемы…………………………………………………………………………………………..30
7. Построение модели «сверху вниз»…………………………………………………………………33
7.1 Что такое примитив?……………………………………………………………………… ….33
7.2 Построение объемных объектов…………………………………………………………………35
7.3 Построение сферы и сферического сегмента………………………………………………… 36
7.4 «Лепка» модели с помощью логических (Булевских) операций…………………………… 36
7.4.1 Хранить или не хранить?……………………………………………………………………….37
7.4.2 Пересечения……………………………………………………………………………………..38
7.4.3 Парные пересечения……………………………………………………………………………..40
7.4.4 Сложение……………………………………………………………………………………… .41
7.4.5 Вычитание…………………………………………………………………………………… …42
7.4.6 Вычитание рабочего поля……………………………………………………………………….48
7.4.7 Классификация…………………………………………………………………………………. .50
7.4.8 Перекрытие……………………………………………………………………………………….50
7.4.9 Разделение……………………………………………………………………………………… 51
7.4.10 Склеивание (или соединение)…………………………………………………………………..52
7.4.11 Альтернатива булевским операциям…………………………………………………………..53
7.4.12 Модернизация после булевских операций…………………………………………………54
7.4.13 Перемещение и копирование объектов твердотельной модели…………………………..56
7.4. 14 Генерация объектов способом симметричного отражения………………………………. 57
7.4.15 Перенос объектов в другую координатную систему…………………………………….. 57
7.4.16 Масштабирование элементов твердотельной модели……………………………………. 58
8. Нагрузки твердотельной модели……………………………………………………………… 59
8.1 Перенос нагрузок…………………………………………………………………………… …59
8.2 Выключение больших символов для узлов и точек……………………………………………60
8. 3 Выбор формата для графического показа нумераций…………………………………… …60
8.4 Печать нагрузок твердотельной модели…………………………………………………… …60
8.5 Расчет массовых и инерциальных характеристик………………………………………………61
9. Соображения и предупреждения по твердотельному моделированию……………………… 62
10. Прямая генерация…………………………………………………………………………………64
10.1 Что такое прямая генерация?……………………………………………………………………64
10.2 Узлы………………………………………………………………………………………………64
10.2.1. Определение узлов……………………………………………………………………………65
10.2.2. Чтение и запись текстовых файлов, содержащих данные об узлах………………………..66
10.3. Элементы……………………………………………………………………………………… 66
10.3.2. Определение элементов………………………………………………………………………68
10.3.3. Использование специальных методов для генерации элементов………………………….69
10.3.4. Чтение и запись текстовых файлов, содержащих данные об элементах………………….70
10.3.5 Замечания о перекрывающихся элементах………………………………………………….70
10.3.6. Модификация элементов……………………………………………………………………..70
10.3.7. Добавление и уничтожение срединных узлов элементов………………………………….71
11. Импорт твердотельных моделей…………………………………………………………………71
11.1. Использование опции DEFAULT………………………………………………………………72
11.2. Импортирование IGES файлов с использованием опции DEFAULT………………………..74
11.3 Исправление топологии………………………………………………………………………….76
11. 4 Установка опций для рисования и печати зазоров…………………………………………….77
11.5 Уничтожение геометрических объектов……………………………………………………….78
11.6 Сшивание зазоров………………………………………………………………………………...78
11.7 Использование инструментов моделирования…………………………………………………80
11.9. Использование инструментальных средств упрощения геометрии……………………….. 95
11.10. Причины возникновения проблем импорта………………………………………………..95
11.11. Ограничения при выборе опции DEFAULT (по умолчанию)……………………………….95
11.12. Использование опции ALTERNATIVE……………………………………………………….96
11.13 Руководящие принципы для использования опции ALTERNATIVE………………………..97
1. Порядок работы в ANSYS
ANSYS имеет много типов конечных элементов, предназначенных для статического анализа, нелинейного анализа, динамического анализа и т. д. Типичный анализ включает три стадии:
Построение модели;
Приложение нагрузок и решение;
Просмотр результатов.
