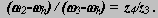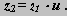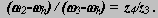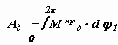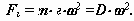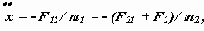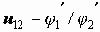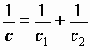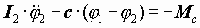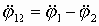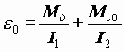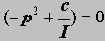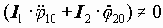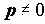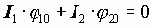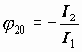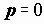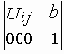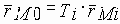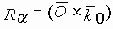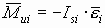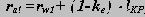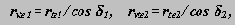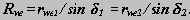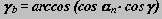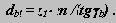называются механизмы с зубчатыми передачами с числом зубчатых колес больше двух. Это могут быть механизмы с оригинальными структурными схемами или механизмы, образованные последовательным и (или) параллельным соединением простейших типовых зубчатых механизмов.
Механизмы, в которых кинематические цепи образуют один или несколько замкнутых контуров и в которых входной поток механической мощности в процессе передачи и преобразования делится на несколько потоков, а затем суммируется на выходном звене, называются
Распределение передаваемых усилий по нескольким кинематическим парам уменьшает нагрузку на элементы пар и позволяет существенно уменьшать габаритные размеры и массу механизмов. Многозонный контакт звеньев механизма существенно увеличивает жесткость механизма, а за счет осреднения ошибок и зазоров, уменьшает мертвый ход и кинематическую погрешность механизма. Однако, за счет образования в структуре механизма внутренних контуров, число избыточных или пассивных связей в механизме увеличивается. Поэтому при изготовлении и сборке механизма необходимо либо повышать точность деталей, либо увеличивать зазоры в кинематических парах.
Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются
К типовым планетарным механизмам относятся:
однорядный планетарный механизм;
двухрядный планетарный механизм с одним внешним и одним внутренним зацеплением
двухрядный планетарный механизм с двумя внешними зацеплениями;
двухрядный планетарный механизм с двумя внутренними зацеплениями.
Элементы планетарного механизма имеют специальные названия:
зубчатое колесо с внешними зубьями, расположенное в центре механизма называется "солнечным";
колесо с внутренними зубьями называют "короной" или "эпициклом";
колеса, оси которых подвижны, называют "сателлитами";
подвижное звено, на котором установлены сателлиты, называют "водилом" .
Звено водила принято обозначать не цифрой, а латинской буквой h.
В таблице 15.1 приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях.
Рядным зубчатым механизмом называется сложный зубчатый механизм с неподвижными осями колес, образованный последовательным соединением нескольких простых зубчатых механизмов. Рассмотрим кинематику рядного механизма составленного из двух зубчатых передач: одной внешнего зацепления и одной внутреннего зацепления. Схема механизма изображена на рис. 15.1.
Напоминание: Для вращательного движения твердого тела относительно оси проходящей через точку А. Примем для размеров масштаб ml, мм/м, а для линейных скоростей - масштаб mV, мм/мЧс-1. Угловая скорость звена i равна
Из основной теоремы зацепления, для первой пары зубчатых колес с внешним зацеплением, можно записать
Передаточное отношение сложного рядного зубчатого, образованного из нескольких соединенных последовательно простых зубчатых механизмов равно произведению передаточных отношений этих механизмов.
Изобразим в масштабе ml, мм/м, кинематическую схему рядного зубчатого механизма. Нанесем на эту схему линейную скорость точки P1, изобразив ее в произвольном масштабе mV, мм/мЧс-1 отрезком Р1Р'1.
Соединим конец этого отрезка точку Р'1 с центрами вращения колес 1 и 2 точками 01 и 02 и получим прямые, определяющие распределение линейных скоростей этих звеньев, для точек лежащих на линии центров. Эти прямые образуют с линией центров соответственно углы y1 иy2 . Точка Р2 является точкой касания начальных окружностей колес 3 и 4. Так как в точке касания начальных окружностей линейные скорости звеньев 2 и 3 равны, а распределение линейных скоростей по линии центров для звена 2 известно, то можно определить отрезок Р2Р'2,который изображает скорость точки Р2 в масштабе mV, мм/мЧс-1. Соединив прямой точку Р'2 с центром вращения звена 3 получим прямую распределения линейных скоростей для точек звена 3, лежащих на линии центров. Угол, который образует эта прямой с линией центров, обозначим y3 . Угловые скорости звеньев определятся из этой схемы по формулам
Передаточное отношение, рассматриваемого рядного зубчатого механизма, будет равно
Формула Виллиса выводится на основании основной теоремы зацепления и устанавливает соотношение между угловыми скоростями зубчатых колес в планетарном механизме. Рассмотрим простейший планетарный механизм с одним внешним зацеплением (см. рис. 15.3). Число подвижностей в этом механизме равно
то есть для получения определенности движения звеньев механизма необходимо сообщить независимые движения двум его звеньям. Рассмотрим движение звеньев механизма относительно стойки и относительно водила. Угловые скорости звеньев в каждом из рассматриваемых движений приведены в таблице 15.2.
В движении звеньев относительно водила угловые скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость водила. Если в движении относительно стойки ось зубчатого колеса 2 подвижна, то в движении относительно водила оси обоих зубчатых колес неподвижны. Поэтому к движению относительно водила можно применить основную теорему зацепления.
Движение механизма относительно стойки
Движение механизма относительно водила
То есть можно записать выражение, которое называется формулой Виллиса для планетарных механизмов
Кинематическое исследование типовых планетарных механизмов графическим и аналитическим методами.
1. Двухрядный механизм с одним внутренним и одним внешним зацеплением.
Дано: Кинематическая схема механизма - ri , числа зубьев колес - zi ; _______________________________________________
Определить: Передаточное отношение механизма - ?
Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис.15.4 на звене 2 нарезаны два зубчатых венца:
z2 , который зацепляется с зубчатым венцом z1 звена 1;
z3 , который зацепляется с внутренним зубчатыми венцом z4 звена 3.
По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес z2 и z1
для внутреннего зацепления колес z4 и z3
Перемножим, правые и левые части этих уравнений, и получим
Графическое определение передаточного отношения.
В системе координат ri0V построим треугольники распределения линейных скоростей звеньев. Для этого из точки А с ординатой r1 в выбранном произвольном масштабе mV, мм/мЧс-1 отложим отрезок a a'. Через конец этого отрезка и начало координат проведем прямую, которая определит распределение скоростей для точек звена 1, лежащих на оси ri. Эта прямая образует с осью ri угол y1. Так как в точке с скорости звеньев 2 и 3 равны между собой и равны нулю, то соединяя точку с с прямой с точкой a', получим линию распределения скоростей для звена 2. Так как точка принадлежит звеньям 2 и h, то ее скорость определяется по лучу с a' для радиуса равного rB = (r1+r2), что в масштабе mV, мм/мЧс-1 соответствует отрезку bb'. Соединяя точку b' с началом координат прямой, найдем линию распределения скоростей для водила. Эта линия образует с осью ri угол yh. Передаточное отношение планетарного механизма определенное по данным графическим построениям можно записать так

2. Однорядный механизм с одним внутренним и одним внешним зацеплением.
Аналитическое определение передаточного отношения.
По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес z2 и z1 :
для внутреннего зацепления колес z2 и z3:
Перемножим, правые и левые части этих уравнений, и получим:
Графическое определение передаточного отношения.
3. Двухрядный механизм с двумя внешними зацеплениями.
Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис.15.6 на звене 2 нарезаны два зубчатых венца:
z2 , который зацепляется с зубчатым венцом z1 звена 1;
z3 , который зацепляется с внутренним зубчатыми венцом z4 звена 3.
По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес z2 и z1 :
для внешнего зацепления колес z4 и z3:
Перемножим, правые и левые части этих уравнений, и получим:
Графическое определение передаточного отношения.
4. Двухрядный механизм с двумя внутренними зацеплениями.
Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис.15.6 на звене 2 нарезаны два зубчатых венца:
z2 , который зацепляется с зубчатым венцом z1 звена 1
; z3 , который зацепляется с внутренним зубчатыми венцом z4 звена 3.
По формуле Виллиса отношение угловых скоростей звеньев для внутреннего зацепления колес z2 и z1 :
для внутреннего зацепления колес z4 и z3:
Перемножим, правые и левые части этих уравнений, и получим:
Графическое определение передаточного отношения.
Кинематическое исследование пространственных планетарных механизмов методом планов угловых скоростей.
Рассмотрим этот метод исследования на примере планетарного механизма конического дифференциала заднего моста автомобиля. На рис. 15.8 изображена схема механизма и планы угловых скоростей.
Планы угловых скоростей строятся в соответствии с векторными уравнениями:
w2=w1+w21;
w4=w3+w43
|
w3=w2+w32;
w5=w3+w53
|
Вектора относительных угловых скоростей направлены по осям мгновенного относительного вращения:
w21- по линии контакта начальных конусов звеньев 2 и 1;
w32- по оси шарнира С;
w43- по линии контакта начальных конусов звеньев 4 и 3;
w53 - по линии контакта начальных конусов звеньев 5 и 3.
Вектора абсолютных угловых скоростей направлены по осям кинематических пар, которые образуют звенья со стойкой:
w2 - по оси пары В ;w1 - по оси пары А ;
w4 - по оси пары Е ; w5 - по оси пары D . Направление угловой скорости сателлита 3 определяется соотношением величин угловых скоростей w2 и w32 . Рассмотрим три режима движения автомобиля:
прямолинейное движение w4 = w5 (векторная диаграмма на рис.15.8a). В этом режиме движения корпус дифференциала 2 и полуоси 4 и 5 вращаются с одинаковыми угловыми скоростями w4 = w5 = w2 , а относительная угловая скорость сателлита w32=0.
поворот автомобиля направо w4 < w5 (векторная диаграмма на рис.15.8б). При повороте направо угловые скорости полуосей не равны и связаны неравенством w4 < w5 ,поэтому сателлит будет вращаться с такой угловой скоростью w32, которая обеспечивает постоянство угловой скорости корпуса дифференциала w2.
буксование левого колеса w4 = 0 (векторная диаграмма на рис.15.8в). При буксовании левого колеса, правое колесо останавливается w4 = 0, а левое будет вращаться с угловой скоростью w5 = 2Ч w2 .
Для того, чтобы в условиях низкого сцепления колес с грунтом, уменьшить опасность их пробуксовывания в дифференциалы автомобилей высокой проходимости включают элементы трения или блокировки.
Установившийся режим движения машины
Краткое содержание: Установившийся режим движения машины. Неравномерность движения и метолы ее регулирования. Коэффициент неравномерности. Маховик и его роль в регулировании неравномерности движения. Решение задачи регулирования хода машины по методу Н.И.Мерцалова. Алгоритм решения прямой задачи динамики при установившемся режиме движения машины. Статическая характеристика асинхронного электродвигателя и ее влияние на неравномерность движения. Устойчивость движения машины с асинхронным электродвигателем.
Установившийся режим движения машины.
Установившийся режим движения машины наступает тогда когда работа внешних сил за цикл не изменяет ее энергии, то есть суммарная работа внешних сил за цикл движения равна нулю.
Установившееся движение Адц = Асц , Ац = D
Т = 0 ,
где
-соответственно работа
за цикл движущих сил и сил сопротивления,
j
10 - начальное значение обобщенной координаты, D
j
ц - приращение обобщенной координаты за цикл.
Рис. 8.1
В пределах цикла текущее значение суммарной работы не равно нулю. Работа может быть то положительной, то отрицательной. При положительной величине работы машина увеличивает свою кинетическую энергию за счет увеличения скорости, то есть разгоняется. На участках, где суммарная работа отрицательна, кинетическая энергия и скорость машины уменьшается, машина притормаживается. В установившемся режиме величины увеличения скорости на участках разгона и снижения на участках торможения за цикл равны, поэтому средняя скорость движения w
1ср = const постоянна. В машинах приведенный момент инерции которых зависит от обобщенной координаты, на неравномерность движения оказывает влияние величина изменения приведенного момента инерции. Колебания скорости изменения обобщенной координаты машины не оказывают прямого влияния на фундамент машины. Поэтому эти колебания и вызывающие их причины определяют, так называемую, внутреннюю виброактивность машины.
Величина амплитуды колебаний скорости D
w
1 определяется разностью между максимальной w
1max и минимальной w
1min скоростями.
За меру измерения колебаний скорости в установившемся режиме принята относительная величина,
которая называется коэффициентом изменения средней скорости
d
= D
w
1 /w
1ср = ( w
1max-- w
1min ) / w
1ср ,
где w
1ср = ( w
1max + w
1min ) / 2 - средняя угловая скорость машины.
Для различных машин в зависимости от требований нормального функционирования (обрыв нитей в прядильных машинах, снижение чистоты поверхности в металлорежущих станках, нагрев обмоток и снижение КПД в электрогенераторах и т.д.) допускаются различные максимальные значения коэффициента изменения средней скорости. Существующая нормативная документация устанавливает следующие допустимые значения коэффициента неравномерности [d
]:
дробилки [d
] = 0.2 ... 0.1;
прессы, ковочные машины [d
] = 0.15 ... 0.1;
насосы [d
] = 0.05 ... 0.03;
металлорежущие станки нормальной точности [d
] = 0.05 ... 0.01;
металлорежущие станки прецизионные [d
] = 0.005 ... 0.001;
двигатели внутреннего сгорания [d
] = 0.015 ... 0.005;
электрогенераторы [d
] = 0.01 ... 0.005;
прядильные машины [d
] = 0.02 ... 0.01 .
Чтобы снизить внутреннюю виброактивность и неравномерность движения применяются различные методы:
уменьшение влияния неравномерности внешних сил ( например, применение многоцилиндровых ДВС, насосов и компрессоров с рациональным сдвигом рабочих процессов в цилиндрах );
уменьшение влияния переменности приведенного момента инерции ( тоже обеспечивается увеличением числа цилиндров в поршневых машинах, а также уменьшением масс и моментов инерции деталей, приведенный момент инерции которых зависит от обобщенной координаты );
установка на валах машины центробежных регуляторов или аккумуляторов кинетической энергии - маховиков;
активное регулирование скорости с использованием систем автоматического управления, включая и компьютерное управление.
Рассмотрим подробно наиболее простой способ регулирования неравномерности вращения - установку дополнительной маховой массы или маховика. Маховик в машине выполняет роль аккумулятора кинетической энергии.
При разгоне часть положительной работы внешних сил расходуется на увеличение кинетической энергии маховика и скорость до которой разгоняется система становится меньше, при торможении маховик отдает запасенную энергию обратно в систему и величина снижения скорости машины уменьшается. Сказанное иллюстрируется графиками, изображенными на рис. 8.2. На этом рисунке: D
w
1 - изменение угловой скорости до установки маховика, D
w
1* - после установки маховика. Отсюда можно сделать вывод: чем больше дополнительная маховая масса, тем меньше изменение D
w
1* и коэффициент неравномерности d
.
Определение закона движения D
w
1 = f ( j
1 ) и приведенного момента инерции IпрI .
Из теоремы об изменении кинетической энергии можно записать
D
T = T - Tнач = А, где D
T = D
TI + D
TII = А и TI = IпрI*w
21/2 .
Если допустить, что D
TI »
dTI , то dTI = IпрI *w
1 * dw
1 . Так как при установившемся движении D
w
1
w
1 , то можно считать что w
1 »
w
1ср . Тогда, переходя к конечным приращениям, получим:
D
TI »
IпрI *w
1ср * D
w
1 , откуда D
w
1 »
D
TI / IпрI *w
1ср .
Так как IпрI *w
1ср = const , то можно записать что D
TImax »
IпрI *w
1ср * D
w
1max, где D
TImax - изменение кинетической энергии первой группы звеньев за цикл, D
w
1max - изменение угловой скорости за цикл. Подставим в эту формулу выражение для коэффициента неравномерности d
= D
w
1max /w
1ср и получим формулу для расчета приведенного момента инерции первой группы, который обеспечивает заданный коэффициент неравномерности
IпрI = D
TImax / (d
*w
1ср2 ) .
Определение момента инерции дополнительной маховой массы (маховика).
Рассмотрим определение маховика для примера рассмотренного в лекции 6 - одноцилиндрового поршневого насоса. В первую группу звеньев в этом примере входят: ротор электродвигателя Iрот, детали редуктора I прред, кривошипный вал I01 и маховик Iм
IпрI = I пррот + I прред + I01 + Iм,
откуда момент инерции маховика
Iм= IпрI - ( I прред + I01 + Iм ).
Решение задачи регулирования хода машины по методу Н.И.Мерцалова.
При расчете маховика (или решении задачи регулирования хода машины) по методу Н.И.Мерцалова задача решается в следующей последовательности:
Определяются параметры динамической модели, например для ДВС Мпрд - приведенный суммарный момент движущих сил и IпрII - приведенный момент инерции второй группы звеньев.
Определяется работа движущих сил Ад интегрированием функции Мпрд = f(j
1) за цикл движения машины (допустим 2p
);
Определяется работа движущих сил за цикл и приравнивается к работе сил сопротивления Адц = Асц. Из этого равенства определяется среднеинтегральное значение момента сил сопротивления
Мпрсср = Асц/ (2p
);
и для него строится диаграмма работы Ас = f(j
1). Суммированием этой диаграммы и диаграммы Ад = f(j
1) получаем диаграмму А = f(j
1).
Делается допущение w
1 »
w
1ср , при котором TII »
IпрII *w
1ср2/ 2 (первое допущение метода Мерцалова), и определяется TII = f(j
1).
Определяется кинетическая энергия первой группы звеньев
TI = А -TII + Tнач = А-TII + TIнач + TIIнач .
Так как начальные значения кинетической энергии неизвестны, то если учесть, что Tнач = TIнач + TIIнач , D
TI = TI - TIнач , D
TII = TII - TIIнач , получим
D
TI = А- D
TII ,
то есть, вычитая из суммарной работы приращение кинетической энергии второй группы, получим приращение кинетической энергии первой группы.
По функции D
TI = f(j
1) определяется максимальное изменение кинетиской энергии за цикл D
TImax . Второй раз делаем допущение w
1 »
w
1ср на основании которого, как показано выше, можно записать
IпрI = D
TImax / (d
*w
1ср2).
Из этого выражения, определив предварительно D
TImax , можно решить две задачи:
задачу синтеза - при заданном [d
] определить необходимый для его обеспечения приведенный момент инерции IпрI нб ,
задачу анализа - при заданном IпрI определить обеспечиваемый им коэффициент неравномерности d
.
Алгоритм решения прямой задачи динамики при установившемся режиме движения машины.
Решение этой задачи рассмотрим на конкретном примере машинного агрегата привода буровой установки.
Дано: Кинематическая схема машины - lAB = 0.12м, lBC = 0.528м, lBS2 = 0.169м, средняя частота вращения кривошипа - w
1ср = 47.124 рад/с2, массы звеньев -
m2 = 24.2 кг, m3 = 36.2 кг, момент инерции - I 2S = 1.21 кг* м2, I 10 = 2.72 кг* м2, максимальное давление в цилиндре - pmax = 4.4 МПа , коэффициент неравномерности вращения [d
] = 1/80 , индикаторная диаграмма (приведена на рис. 8.3) .
_________________________________________________________________
Определить: закон движения машины w
1 = f(j
1) и e
1 = f(j
1), момент инерции маховика Iдоп , обеспечивающий заданную неравномерность вращения [d
].
Определение параметров динамической модели: Мпрд - приведенного суммарного момента движущих сил и IпрII - приведенного момента инерции второй группы звеньев.
Определение первых кинематических передаточных функций. Определение кинематических передаточных функций для звеньев механизма u21 = u31 , центров масс VqS1 , VqS2 и VqS3 и точки приложения движущей силы VqD . Для определения этих функций воспользуемся методом проекций векторного контура механизма .
Рассмотрим следующие векторные контуры, изображенные на рис. 8.4 рядом со схемой механизма:
l AB + l CB = l AC ; l AS2 = l AB + l BS2 .
Для первого векторного контура l AB+ l CB = l AC проекции на оси координат
lAB * cos j
1 + lCB * cos j
2 = xC = 0,
lAB * sin j
1 + lCB * sin j
2 = yC = SC,
j
2 = arccos ( - lAB * cos j
1 / lBC ).
Рис. 8.4
Производные от этих выражений
- lAB * sin j
1 - lCB * u21* sin j
2 = 0 ,
lAB * cos j
1 + lCB * u21* cos j
2 = VqC ,
позволяют определить первые передаточные функции
u21 = - lAB * sin j
1 / ( lCB* sin j
2 ),
VqC = lAB * cos j
1 + lCB * u21* cos j
2 .
Для третьего векторного контура l AS2 = l AB + l BS2 проекции на оси координат
xS2 = lAB * cos j
1 + lBS2 * cos j
2 ,
yS2 = lAB * sin j
1 + lBS2 * sin j
2 .
Производные от этих выражений
VqS2x = - lAB * sin j
1 - lBS2 * u21* sin j
2 ,
VqS2y = lAB * cos j
1 + lBS2 * u21* cos j
2 ,
позволяют определить первую передаточную функцию
Рис. 8.5
1.2. Определение приведенного момента движущих сил Мпрд .
Индикаторную диаграмму (рис.8.3) строим по заданным значениям давления в цилиндре двигателя.
Отрезок хода поршня НC* m
i делим на 10 интервалов. В каждой точке деления строим ординату диаграммы, задавшись (при pi /pmax = 1) максимальной ординатой ypmax . Тогда текущее значение ординаты
ypi= ypmax * ( pi/pmax ),
где pmax= 4.4 МПа.
Масштаб индикаторной диаграммы
m
p = ypmax /pmax .
Площадь поршня Sп = p
*dп2 /4 .
При построении графика силы, действующей на поршень, ординаты этого графика принимаем равными ординатам индикаторной диаграммы. Тогда масштаб силы
m
F = m
p/Sп.
Для исследуемого механизма приведенный суммарной момент состоит из двух составляющих: движущей силы и момента сил сопротивления
Mпр = Mпрд + Mпрс .
Приведенный момент движущей силы определяется в текущем положении механизма по формуле
где F дi - значение движущей силы,
F дi = yFдi / m
F ,
где yFдi - ордината силы сопротивления,
m
F - масштаб диаграммы сил.
VqСi - значение передаточной функции в рассматриваемом положении механизма,
- угол между вектором силы и вектором скорости точки ее приложения.
Масштаб диаграммы по оси абсцисс определяется по формуле
m
j
= b / 2*p
,
где b - база диаграммы ( отрезок оси абсцисс, который изображает цикл изменения обобщенной координаты).
1.3. Построение диаграммы приведенных моментов инерции Ivпр = I IIпр.
Инерционные характеристики звеньев механизма в его динамической модели представлены суммарным приведенным моментом инерции. При расчете эту характеристику динамической модели представляетсяв виде суммы двух составляющих переменной Ivпр = I IIпр и постоянной Icпр = IIпр. Первая определяется массами и моментами инерции звеньев, передаточные функции которых постоянны, вторые - массами и моментами инерции звеньев передаточные функции которых переменны.
Проведем расчет переменной части приведенного момента инерции Ivпр = I IIпр. Для рассматриваемого механизма во вторую группу звеньев входят звенья 2 и 3. Звено 3 совершает поступательное движение, звено 2 -плоское. Расчет переменной части приведенного момента проводится по следующим зависимостям:
Ivпр = I IIпр = I2Впр + I2Ппр+ I3пр,
где
I2Ппр = m 2 * VqS22, I2Впр = IS2 * u212, I3пр= m3* VqС2,
Рис. 8.7
2. Построение диаграмм работы движущей силы, сил сопротивления и суммарной работы. Диаграмму работы движущей силы получим интегрируя диаграмму ее приведенного момента
Интегрирование проведем графическим методом (рис.8.8), приняв при этом отрезок интегрирования равным k1 . Тогда масштаб полученной диаграммы работы движущей силы будет равен
tg y
1 = yD
Aд / xD
j
1 = yMпрд1/ k1 D
Aд * m
А/ (D
j
1 * m
j
) = Mпр д1 * m
М / k1
так как D
Aд / D
j
1 = Mпр д1 , то m
А / m
j
= m
М / k1 , откуда
m
А = m
М *m
j
/ k1 .
Величина среднеинтегрального момента сил сопротивления определяется по формуле
Мпрсср = Асц/ (2p
).
3. Построение диаграмм кинетических энергий.
Диаграммы кинетических энергий для первой и второй групп звеньев получает на основании теоремы об изменении кинетической энергии системы
D
Т = Т - Тнач, A = D
Т I + D
Т II .
График кинетической энергии второй группы звеньев получим из зависимости
Т II = III пр*w
1ср2 /2,
принимая, что w
1 »
w
1ср . Тогда диаграмма приведенного момента инерции второй группы звеньев в масштабе рассчитанном по формуле
yI = yT IпрII * m
I = (IпрII * w
1ср2 / 2) * m
T , откуда
m
T = 2* m
I /w
1ср2 ,
соответствует диаграмме кинетической энергии ТII .
График кинетической энергии первой группы звеньев приближенно строим по уравнению
ТI = Т - ТII .
В каждом положении механизма из ординат кривой A= f (j
1) вычитаем ординаты yTII и получаем ординаты искомой диаграммы TI = f (j
1). Для этого необходимо ординаты диаграммы TII = f (j
1) из масштаба m
T перевести в масштаб m
A* по формуле
yTII* = yTII * m
A*/ m
T .
Диаграмма кинетической энергии первой группы звеньев представлена на рис. 8.9.
4. Определение необходимого момента инерции маховых масс первой группы
Максимальное изменение кинетической энергии звеньев перD
вой группы за цикл определяем по диаграмме
D
TImax = ( y D
TImax )/ m
A .
Тогда необходимый момент инерции маховых масс первой группы звеньев, обеспечивающий заданный коэффициент неравномерности, равен
IIпр = D
TImax / (w
1ср2 * [d
] ) .
4.1. Определение момента инерции дополнительной маховой массы.
В нашем случае момент инерции дополнительной маховой массы рассчитывается по следующей зависимости
Iдоп = IIпр - I10 ,
где I10 - момент инерции коленчатого вала .
5. Построение приближенной диаграммы угловой скорости
Если считать, что w
1 »
w
1ср , то
D
TI = IIпр *w
1ср * D
w
1,
то есть диаграмма изменения кинетической энергии первой группы звеньев D
TI= f(j
1) в другом масштабе соответствует диаграмме изменения угловой скорости D
w
1 = f (j
1). Если считать что ординаты диаграмм равны, то
yD
w
1 = yD
TI m
A* D
TI = m
w
* D
w
1 m
A* IIпр *w
1ср * D
w
1 = m
w
* D
w
1 ,
откуда
m
w
= m
A* IIпр *w
1ср .
Ордината средней угловой скорости ( для определения положения начала координат на диаграмме угловой скорости )
yw
1ср = w
1ср *m
w
.
После определения положения оси абсцисс на диаграмме угловой скорости можно определить начальное значение угловой скорости
w
10 = yw
10 /m
w
,
а по ней кинетическую энергию механизма в начальном положении
TI нач = IIпр *w
1ср2 /2 .
6. Определение размеров маховика.
Принимаем конструктивное исполнение маховика - диск. Тогда его основные размеры и масса определятся по следующим зависимостям:
наружный диаметр
ширина b = y
b * D ,
масса m = 1230* D 3,
где r
= 7.8 кг/дм3 - плотность материала маховика ,
y
b - коэффициент ширины .
7. Определение углового ускорения звена приведения.
Как отмечено ранее для расчета углового ускорения звена приведения e
1 = f(j
1 ) лучше пользоваться формулой :
e
1 = dw
1/dt = М пр/ Iпр- w
12/(2* Iпр) * (d Iпр /dj
1).
Необходимые для расчета значения величин определяем по ранее построенным диаграммам. Диаграмма функции e
1 = f(j
1 ) приведена на рис. 8.10.
Рис. 8.10
Приведенная статическая характеристика асинхронного электродвигателя. Понятие о устойчивости работы машины.
Как отмечалось ранее, силы действующие на механизмы зависят не только от положения или обобщенной координаты, а зависят и от времени или от скорости.
Эти зависимости обычно определяются экспериментально и называются механическими характеристиками машины. Механическая характеристика приведенная к обобщенной координате или скорости называется приведенной механической характеристикой. В качестве примера рассмотрим приведенную статическую характеристику асинхронного электродвигателя.
На диаграмме: М прдп - приведенный пусковой момент; М прдн - приведенный номинальный крутящий момент; М прдк или М прдmax - приведенный критический или максимальный момент; w
1н - номинальная круговая частота вращения звена приведения; w
1хх или w
1с - частота вращения звена приведения на холостом ходу или синхронная. Уравнение приведенной статической характеристики асинхронного электродвигателя на линеаризованном участке устойчивой части
М прд = b1* + k1**w
1 ,
где М прд - приведенный движущий момент на звене приведения,
w
1 - круговая частота звена приведения ,
b1* = М прдн * w
1 /(w
1с - w
1н ) , k1* = - М прдн / (w
1с - w
1н ).
Как на исходной статической характеристике двигателя, так и на приведенной можно выделить два участка: устойчивый - bd и неустойчивый - ab. На устойчивом участке при увеличении момента сопротивления на валу двигателя частота вращения уменьшается, обеспечивая сохранение мощности примерно на постоянном уровне, на неустойчивом участке работа двигателя невозможна, так как в любой точке этого участка увеличение момента сопротивления на валу двигателя должно сопровождаться увеличением частоты вращения и увеличением мощности двигателя, при этом моменты сопротивления больше пускового момента двигателя. При увеличении момента сопротивления на валу звена приведения до величины большей Мпрдmax двигатель попадает в зону неустойчивой характеристики и останавливается. Для устойчивой работы машины необходимо, чтобы колебания момента сопротивления на
валу звена приведения не выходили за пределы линейной части устойчивого участка приведенной статической характеристики.
Учет приведенной статической характеристики при анализе
Вибрации и колебания в машинах и механизмах
Краткое содержание: Вибрации и колебания в машинах и механизмах, виброактивность и виброзащита. Понятие о неуравновешенности звена и механизма, статической и динамической уравновешенности механической системы. Статическое уравновешивание рычажных механизмов. Метод замещающих масс. Полное и частичное статическое уравновешивание механизма. Ротор и виды его неуравновешенности: статическая, моментная и динамическая. Балансировка роторов при проектировании. Балансировочные станки.
Вибрации и колебания в машинах и механизмах.
При движении механической системы под действием внешних сил в ней могут возникать механические колебания или вибрации. Причинами возникновения вибраций могут быть периодические изменения сил (силовое возмущение), перемешений (кинематическое возмущение) или инерционных характеристик (параметрическое возмущение). Вибрацией ( от лат. vibratio - колебание ) называют мех*анические колебания в машинах или механизмах. Колебание - движение или изменение состояния, обладающие той или иной степенью повторяемости или периодичностью. Если источник возникновения вибраций определяется внутренними свойствами машины или механизма, то говорят о его виброактивности. Чтобы вибрации механизма не распространялись на окружающие его системы или чтобы защитить механизм от вибраций, воздействующих на него со стороны внешних систем, применяются различные методы виброзащиты. Различают внешнюю и внутреннюю виброактивность. Под внутренней виброактивностью понимают колебания возникающие внутри механизма или машины, которые происходят по его подвижностям или обобщенным координатам. Эти колебания не оказыват непосредственного влияния на окрущающую среду. При внешней виброактивности изменение положения механизма приводит к изменению реакций в опорах (т.е. связях механизма с окружающей средой) и непосредственному вибрационному воздействию на связанные с ним системы. Одна и основных причин внешней виброактивности - неуравновешенность его звеньев и механизма в целом.
Понятие о неуравновешенности механизма (звена).
Неуравновешенным будем называть такой механизм (или его звено), в котором при движении центр масс механизма (или звена) движется с ускорением.
Так как ускоренное движение системы возникает только в случае, если равнодействующая внешних силовых воздействий не равна нулю. Согласно принципу Д’Аламбера, для уравновешивания внешних сил к системе добавляются расчетные силы - силы и моменты сил инерции. Поэтому уравновешенным будем считать механизм, в котором главные вектора и моменты сил инерции равны нулю, а неуравновешенным механизм, в котором эти силы неравны нулю. Для примера рассмотрим четырехшарнирный механизм (рис. 5.1).
Механизм будет находится в состоянии кинетостатического равновесия, если сумма действующих на него внешних сил и моментов сил (включая силы и моменты сил инерции) будет равна нулю
Уравновешенность является свойством или характеристикой механизма и не должна зависеть от действующих на него внешних сил. Если исключить из рассмотрения все внешние силы, то в уравнении равновесия останутся только инерционные составляющие, которые определяются инерционными параметрами механизма - массами и моментами инерции и законом движения (например, центра масс системы). поэтому уравновешенным считается механизм для которого главный вектор и главный момент сил инерции равны нулю:
Неуравновешенность - такое состояние механизма при котором главный вектор или главный момент сил инерции не равны нулю. Различают:
статическую неуравновешенность FSм не равно 0 ;
моментную неуравновешенность Mимне равно 0 ;
динамическую неуравновешенность FSм?не равно 0 и Mимне равно 0 .
При статическом уравновешивании механизма необходимо обеспечить
Это условие можно выполнить если: скорость центра масс механизма равна нулю VSм=0или она постоянна по величине и направлению VSм= const.
Обеспечить выполнение условия VSм = const в механизме практически невозможно. Поэтому при статическом уравновешивании обеспечивают выполнение условия VSм=0 . Это возможно, когда центр масс механизма лежит на оси вращения звена 1 - rSм= 0 или когда он неподвижен rSм= const , где rSм= ( m1*rS1
+ m2*rS2 + ... + m*rSi )/ (m1 + m2 + ... + mi).
На практике наиболее часто статическое уравновешивание проводят:
выбирая симметричные схемы механизма (рис.5.2);
устанавливая на звеньях механизма противовесы (или корректирующие массы);
размещая противовесы на дополнительных звеньях или кинематических цепях.
Метод замещающих масс.
При использовании метода замещающих масс, звено механизма с распределенной массой заменяется расчетной моделью, которая состоит из точечных масс.
Условия перехода от звена с распределенной массой к модели с точечными массами.
Сохранение массы звена: m iA + m iB = mi .
Сохранение положения центра масс lASi = const , m iA *lASi = m iB*(lAB - lASi).
Сохранение момента инерции
m iA*lASi2 + m iB *(lAB - lASi)2 = Isi.
Очевидно, что выполнить три условия системой с двумя массами невозможно, поэтому при статическом уравновешивании механизмов ограничиваются выполнением только двух первых условий. Чтобы обеспечить выполнение всех трех условий необходимо ввести третью массу m iSi. Рассмотрим применение метода замещающих масс при полном и частичном статическом уравновешивании кривошипно-ползунного механизма. Полное статическое уравновешивание кривошипно- ползунного механизма.
Постановка задачи: Дано: lAB, lBC, lAS1, lBS2, lCS3=0, m1, m2, m3
Определить: mk1, mk2
Распределим массы звеньев по методу замещающих масс и сосредоточим их в центрах шарнировA,B,C.Тогда mB = mB1 + mB2 , m C = m3 + mC2 , mA = mA1 ,
где m1 = mA1 + mB1 - масса первого звена, распределенная между массами, сосредоточенными в точках В ; m2 = mВ2 + m - масса второго звена, распределенная между массами, сосредоточенными в точках В и С
Вначале проведем уравновешивание массы mC корректирующей массой mk2. Составим уравнение статических моментов относительно точки В для звеньев 2 и 3: m k2 lk2 = m C lBC .
Задаемся величиной lk2 и получаем корректирующую массу m k2 = m C *lBC / lk2 .
Затем уравновешиваем массы центр, которых после установки корректирующей массы расположился в точке В: mB * = m2 + mk2 + m3 + mB1. Составляем уравнение статических моментов относительно точки А
m k1*lk1 = mВ* ?
lАВ . Задаемся величиной lk1 и получаем корректирующую массу
m k1 = mВ*lАВ / lk1.
Окончательно величины корректирующих масс для полного уравновешивания кривошипно-ползунного механизма m k2 = m C *lBC / lk2 = ( mС2 + m3 )* lBC / lk2 ;
m k1 = mВ*lАВ / lk1= (m2 + mk2 + m3 + mB1)
*lАВ / lk1 .
Частичное статическое уравновешивание кривошипно-ползунного механизма.
Уравновешивание вертикальной составляющей главного вектора сил инерции.
Постановка задачи: Дано: lAB, lBC, lAS1, lBS2, lCS3=0,
m1, m2, m3
Определить: mk1
В этом случае необходимо добиться, чтобы центр масс механизма при движении перемещался вдоль направляющей ползуна (для схемы на рис. 5.5 по горизонтали). Для этого достаточно уравновесить только массу mB .
Составляем уравнение статических моментов относительно точки А : m k1 *lk1 = mВ *lАВ . Задаемся величиной lk1 и получаем корректирующую массу m k1 = mВ *lАВ / lk1. Окончательно величина корректирующей массы для уравновешивания вертикальной составляющей главного вектора сил инерции кривошипно-ползунного механизма m k1 = mВ *lАВ / lk1= (m
В2 + mB1) *lАВ / lk1 .
2. Уравновешивание горизонтальной составляющей главного вектора сил инерции.
Постановка задачи:
Дано: lAB, lBC, lAS1, lBS2,
lCS3=0, m1, m2, m3
Определить: mk1
В этом случае необходимо добиться, чтобы центр масс механизма при движении перемещался по дуге окружности радиуса rSм (рис.5.6). Расчет корректирующей массы ведется в два этапа. В начале первой составляющей корректирующей массы mk1 уравновешивается масса mB . Составляется, как и в предыдущем примере, уравнение статических моментов относительно точки А : m k1
lk1 = mВ lАВ . Задается величина lk1 и рассчитывается корректирующая масса m k1= mВ lАВ / lk1= (mВ2 + mB1) * lАВ / lk1 .
Затем с помощью второй составляющей корректирующей массы mk1центр массы mc
перемещается в точку Sм. Величина mk1 определяется следующим образом: центр шарнира С соединяется прямой с концом отрезка lk1 точкой Sk . Радиус rSм проводится параллельно отрезку B С. Тогда SkВС = Sk
А Sми x/y =. lk1 / lAB
Статический момент относительно точкиSм: mk1
x = mCy, mk1 = mC y/x = mC lAB / lk1 .
Радиус-вектор rSм определяется из подобия треугольников из пропорций x/ rSм= ( x + y )/ lBC , x/( x + y ) = lk1 / ( lk1 + lAB ),
откуда rSм= [ lk1 / ( lk1 + lAB )]*lBC = const.
Корректирующая масса, обеспечивающая уравновешивание горизонтальной составляющей главного вектора сил инерции кривошипо-ползунного механизма, размещается на первом звене механизма и равна сумме составляющих mk1 = mk1+ mk1 = ( m2 + m3 + mB1 )lАВ / lk1 .
Центр массы механизма при таком уравновешивании расположен в точкеSм, которая движется по дуге радиуса rSм
rSм= ( mС2+ m3 + mk1) rSм/( m1 + m2 + m3 + mk1 ).
Схема распределения масс в механизме после уравновешивания дана на рис. 5.7.
Балансировка роторов.
Общие сведения о балансировке.
Ротор, неуравновешенность ротора и ее виды. Задачи балансировки.
Ротором ( по гост 19534-74 ) называют звенья механизмов, совершающие вращательное движение и удерживаемые при этом своими несущими поверхностями в опорах. Если масса ротора распределена относительно оси вращения равномерно, то главная центральная ось инерции x-x совпадает с осью вращения и ротор является уравновешенным или идеальным. При несовпадении оси вращения с осью x-x, ротор будет неуравновешенным и в его опорах при вращении возникнут переменные реакции, вызванные действием инерционных сил и моментов ( точнее, движением центра масс с ускорением ).
В зависимости от взаимного расположения оси вращения и главной цетральной оси инерции x-x , по ГОСТ 19534-74, различают следующие виды неуравновешенности роторов (рис. 5.8): а - статическую, когда эти оси параллельны; б - моментную, когда оси пересекаются в центре масс ротора S; в - динамическую, когда оси либо пересекаются вне центра масс, либо не пересекаются, а перекрещиваются в пространстве. Как отмечено выше, неуравновешенность определяется конструктивными характеристиками ротора или механизма и не зависит от параметров движения. Поэтому при балансировке оперируют не инерционными силами, а дисбалансами.
Дисбаланс - мера статической неуравновешенности ротора, векторная величина, равная произведению неуравновешенной массы m на ее эксцентриситет e, где эксцентриситет e - радиус-вектор центра этой массы относительно оси ротора. Направление главного вектора дисбаланса D совпадает с направлением главного вектора сил инерции Fи, действующих на ротор при вращении:
Моментная неуравновешенность характеризуется главным моментом дисбалансов ротора MD , который пропорционален главному моменту сил инерции (рис. 5.9):
Главный момент дисбалансов ротора полностью определяется моментом пары равных по величине и противоположных по направлению дисбалансов DM1 + DM2 = DM, расположенных в двух произвольных плоскостях ( I и II ), перпендикулярных оси вращения ротора.
Дисбаланс и момент дисбалансов не зависят от частоты вращения, они полностью определяются конструкцией ротора и точностью его изготовления. Балансировкой называют процесс определения значений и угловых координат дисбалансов ротора и их уменьшения с помощью корректировки размещения его масс. Балансировка эквивалентна уравновешиванию системы инерционных сил, прикладываемых к подвижному ротору для его равновесия.
Эту систему, как и любую произвольную систему сил, можно заменить равнодействующими - главным вектором и главным моментом или двумя векторами, расположенными в произвольных параллельных плоскостях. Для уравновешивания системы сил достаточно уравновесить эти равнодействующие. При балансировке операции над силами заменяют действиями над дисбалансами. Поэтому для жестких роторов выщесказанное можно сформулировать так: жесткий ротор можно уравновесить двумя корректирующими массами, расположенными в двух произвольно выбранных плоскостях, перпендикулярных оси его вращения. Эти плоскости называют плоскостями коррекции.
Задача балансировки ротора заключается в определении, в выбранных плоскостях коррекции , значений и углов дисбалансов и размещении в этих плоскостях корректирующих масс, дисбалансы которых равны по величине и противоположны по направлению найденным дисбалансам ротора. На практике балансировку проводят : при конструировании - расчетными методами, в процессе изготовления деталей и узлов - экспериментально на специальных балансировочных станках. Балансировка на станках является более точным и надежным методом, по сравнению с расчетными. Поэтому она применяется для ответственных деталей с высокими рабочими частотами вращения. Корректировка масс ротора осуществляется либо присоединением к нему дополнительных корректирующих масс (наплавлением, наваркой или привинчиванием противовесов), либо удалением части массы ротора с “тяжелой” стороны (фрезерованием или высверливанием). Точность балансировки характеризуется величиной остаточного дисбаланса D0 ротора в каждой из плоскостей коррекции.
Величина D0 не должна превышать допустимых для данного класса точности значений, регламентируемых ГОСТ 22061-76.
Балансировка роторов при различных видах неуравновешенности.
1. Статическая неуравновешенность.
При статической неуравновешенности (рис.5.10) главная центральная ось инерции параллельны оси вращения ротора , главный вектор дисбалансов больше нуля , а главный момент дисбалансов равен нулю Dс0 ; MD = 0,
т.е. необходимо уравновесить только вектор Dс= m e.
Для этого достаточно установить на роторе только одну корректирующую массу mk величине которой определяется из равенства Dk = mk ek = -Dc mk = Dk / ek , где величиной ek задаются из соображений удобства размещения противовесов. Направление вектора Dk противоположно направлению Dc .
Условие статической уравновешенности ротора: 2.2. Моментная неуравновешенность.
При моментной неуравновешенности (рис.5.11) главная центральная ось инерции пересекает ось вращения в центре масс ротора точке S, главный вектор дисбалансов Dс равен нулю, гавный момент дисбалансов МD не равен нулю т.е. необходимо уравновесить только момент дисбалансов МD . Для этого достаточно разместить на роторе две одинаковых корректирующих массы mk на равных расстояниях от оси вращения ek и от ценра масс S - lk. Массы выбираются и размещаются так, чтобы момент их дисбалансов MDk был по величине равен, а по направлению противоположен моменту дисбалансов ротора МD:
где Dk = mk ek .
В этих зависимостях величинами lk
и ek задаются по условиям удобства размещения противовесов на роторе, а величину mk рассчитывают. Необходимо отметить, что величины Dk в плоскостях коррекции необязательно должны быть равными, необходимо выполнять только неизменность положения центра масс - он должен оставаться на оси вращения.
Условие моментной неуравновешенности 2.3. Динамическая неуравновешенность.
При динамической неуравновешенности (pис. 5.12) главная центральная ось инерции пересекает ось вращения не в центре масс ротора точке S, либо перекрещивается с ней; и главный вектор дисбалансов Dc, и главный момент дисбалансов МD не равны нулю т.е.
необходимо уравновесить вектор Dс и момент дисбалансов МD . Для этого достаточно разместить на роторе две корректирующих массы mk1 и mk2 на расстояниях от оси вращения ek1 и ek2 , а от ценра масс S, соответственно на lk1 и lk2. Массы выбираются и размещаются так, чтобы момент их дисбалансов MDk был по величине равен, а по направлению противоположен моменту дисбалансов ротора МD:
где
а векторная сумма дисбалансов была равна и противоположно направлена вектору Dc:
B этих зависимостях величинами lki и eki задаются по условиям удобства размещения противовесов на роторе, а величины mki рассчитывают.
Условие динамической уравновешенности ротора: 3. Уравновешивание роторов при проектировании. 1. Статическое уравновешивание при проектировании.
При проектировании статически уравновешивают детали, имеющие небольшие осевые размеры и конструктивно неуравновешенные, например, дисковые кулачки (рис. 5.13) Когда кулачок неподвижен w1= 0 , реакция в опоре F10 = - G. При вращении кулачка , реакция в опоре равна векторной сумме сил тяжести и центробежной силы инерции
При проектировании детали типа кулачка уравновешиваются так: в деталь с центром на оси вращения вписывается окружность, подсчитываются площади ограниченные контуром кулачка и расположенные вне или внутри окружности, определяется массы и центры масс Sn неуравновешенных частей кулачка, находится эксцентриситет e1 центра масс S1 кулачка по величине и направлению и определяется его дисбаланс с помощью корректирующей массы mk, размещаемой на эксцентриситете ek, создается дисбаланс Dk равный по величине и противоположный по направлению D1.
Динамическое уравновешивание при проектировании.
Динамическое уравновешивание при проектировании проводят с деталями и узлами, в которых массы распределены относительно оси вращения неравномерно, например, детали типа коленчатого вала. Эти детали делят на несколько дисков и в каждом диске, также как при статическом уравновешивании, определяют величину и направле ние дисбаланса Di .
На детали выбирают две плоскости коррекции и каждый вектор дисбаланса расклад ывают на две составляющие, расположенные в плоскостях коррекции.Затем составляю щие векторы дисбалансов в плоскостях коррекции суммируются и их равнодействующи й дисбаланс, например, DI, уравновешивается соответств ующей корректирующей массой mIk . Пример такого уравновешивания изображен на рис. 5.14.
Схема размещения корректирующих масс в плоскостях коррекции.
Виброзащита машин и механизмов
Краткое содержание: Виброзащита машин и механизмов. Методы виброзащиты. Взаимодействие двух подвижных звеньев. Подрессоривание и виброизоляция. Динамическое гашение колебаний. Трение в механизмах. Виды трения. Силы в кинематических парах с учетом трения. Силовой расчет механизмов с учетом сил трения. Понятие о КПД механической системы. КПД механической системы при последовательном и параллельном соединении механизмов. Приложение: Метод планов положений, скоростей и ускорений при анализе простейшего кулисного механизма.
Виброзащита в машин и механизмов.
Как отмечалось ранее, при движении механической системы под действием внешних сил в ней возникают механические колебания или вибрации. Эти вибрации оказывают влияние на функционирование механизма и часто ухудшают его эксплуатационные характеристики: снижают точность, уменьшают КПД и долговечность машины, увеличивают нагрев деталей, снижают их прочность, оказывают вредное воздействие на человека-оператора. Для снижения влияния вибраций используют различные методы борьбы с вибрацией. С одной стороны при проектировании машины принимают меры для снижения ее виброактивности (уравновешивание и балансировка механизмов), с другой - предусматриваются средства защиты как машины от вибраций, исходящих от других машин (для рассматриваемой машины от среды), так среды и операторов от вибраций данной машины.
Методы виброзащиты.
Существующие виброзащитные устройства по методу снижения уровня вибраций делятся на:
динамические гасители или антивибраторы, в которых опасные резонансные колебания устраняются изменением соотношения между собственными частотами системы и частотами возмущающих сил;
виброизоляторы, в которых за счет их упругих и демпфирующих свойств уменьшается амплитуда колебаний как на резонансных и нерезонансных режимах.
Взаимодействие двух подвижных звеньев.
Рассмотрим механическую систему (рис. 9.1), состоящую из двух подвижных звеньев, образующих между собой кинематическую пару.
Для упрощения предположим, что движение звеньев возможно только по одной координате x. Масса первого звена m1 , второго - m2 . На звено 2 действует периодическая внешняя сила F2 = F20
*sin wt , действием сил веса принебрегаем Уравнения движения звеньев
Если считать, что контакт между звеньями в процессе движения не нарушается и тела абсолютно жесткие, то
x = x1 = x2
С учетом F21 = - F12, определим реакцию в точке контакта между звеньями
Откуда
и после преобразований
F21 (m1 + m2)/(m1+ m2) = - F2 / m2 ,
F21 = - F2* m1 / (m1 + m2).
Проанализируем эту зависимость:
если m1 => 0, то F21 => 0 ; если m2=> 0 , то F21 => F2 ;
если m2 = m1 = m , то F21 => - 0.5*F2 ;
если m2 =>?
, то F21 => 0 ;
eсли m1 => ?
, то F21 => - F2 .
Анализ показывает, что реакция взаимодействия между звеньями зависит от соотношения их масс и величины внешней силы. При этом кинетическая энергия системы

Подрессоривание или виброизоляция.

В этой механической системе x2
>x1 ( предположим, что x2 > x1 ) и D
x = x2 - x1 , тогда кинетическая энергия системы

U = c* D
x2 / 2.
То есть в системе с виброизолятором только часть работы внешней силы расходуется на изменение кинетической энергии. Часть этой работы переходит в потенциальную энергию упругого элемента и часть рассеивается демпфером (переходит в тепло и рассеивается в окружающей среде).
Уравнения движения


Динамическое гашение колебаний.
Динамические гасители или антивибраторы широко применяются в машинах работающих в установившихся режимах для отстройки от резонансных частот (например, в судовых двигателях внутреннего сгорания).
Динамические гасители могут быть выполнены в виде упругого или физического маятника. Рассмотрим простейший линейный упругий динамический гаситель (рис.9.4). Принцип действия динамического гасителя заключается в создании гасителем силы направленной противоположно возмущающей силе. Настройка динамического гасителя заключается в подборе его собственной частоты: собственная частота гасителя должна быть равна частоте тех колебаний, амплитуду которых необходимо уменьшить (“погасить”)

Уравнения движения системы с динамическим гасителем, схема которого изображена на рис. 9.4

На рис. 9.5 приведены амплитудно-частотные характеристики этой системы без динамического гасителя и с динамическим гасителем. Как видно из этих характеристик, при установке динамического гасителя амплитуда на частоте настройки резко снижается, однако в системе вместо одной собственной частоты возникает две. Поэтому динамические гасители эффективны только в узком диапазоне частот вблизи частоты настройки гасителя. Изображенные на рисунке кривые 1 и 2 относятся к динамическому гасителю без демпфирования. При наличии в системе демпферов форма кривой изменяется (кривая 3): амплитуды в зонах гашения увеличиваются, а зонах резонанса - уменьшаются.
Подробнее с вопросами виброзащиты машин можно познакомиться в учебной [ 9.1, 9.2 ] или специальной литературе [ 9.3 , 9.4 ].
Трение в механизмах. Виды трения.
Способность контактирующих поверхностей звеньев сопротивляться их относительному движению называется внешним трением. Трение обусловлено неидеальным состоянием контактирующих поверхностей (микронеровности, загрязнения, окисные пленки и т.п.) и силами межмолекулярного сцепления. Трение в кинематических парах характеризуется силами трения и моментами сил трения. Силой трения называется касательная составляющая реакции в КП (составляющая направленная по касательной к контактирующим поверхностям), которая всегда направлена против вектора скорости относительного движения звеньев.
Различают следующие виды трения:
трение покоя проявляется в момент, когда два тела находящиеся в состоянии относительного покоя начинают относительное движение (касательную составляющую возникающую в зоне контакта до возникновения относительного движения, в условиях когда она меньше силы трения покоя, будем называть силой сцепления; максимальная величина силы сцепления равна силе трения покоя);
трение скольжения появляется в КП при наличии относительного движения звеньев; для большинства материалов трение скольжения меньше трения покоя;
трение качения появляется в высших КП при наличии относительного вращательного движения звеньев вокруг оси или точки контакта;
трение верчения возникает при взаимодействии торцевых поверхностей звеньев вращательных КП (подпятники).
Кроме того по наличию и виду применяемых смазочных материалов различают:


Fтр ij = f ?
F nij ,
где f - коэффициент трения скольжения .
Силы в кинематических парах с учетом трения.
1. Поступательная КП (рис.9.7).

реактивный момент Mij ,
величина реакции Fij ;
направление вектора Fij ;
известны: точка приложения силы - геометрический центр кинематической пары A1п. и коэффициент трения скольжения f .
Полная величина реакции в КП равна векторной сумме
где Fтр ij = F nij *tg j
= F nij *f - сила трения скольжения, j
- угол трения , f - коэффициент трения скольжения (tg j
»
f , так как j
мало).
Если tg j
»
f =>
0, то Fij => F nij , т.е. к решению без учета трения.
Число неизвестных в поступательной КП при силовом расчете с учетом трения увеличилось и равно ns = 3.
2. Вращательная КП
Силовой расчет с учетом трения является моделью КП более высокого уровня, с большей степенью приближения модели к реальной КП. При этом известны геометрические размеры элементов КП (радиусы цапф) и коэффициент трения скольжения. Так как в реальных парах имеются зазоры, то на расчетной схеме (рис.9.8) пару представляют как высшую.
При силовом расчете c учетом трения во вращательной КП определяются:
направление реакции Fij ;
величина реакции Fij ;
величина силы трения Fтр ij;
<>известно: линия действия нормальной составляющей проходит через центр КП точку B1в. , коэффициент трения скольжения , радиус цапфы ri »
rj .
Момент трения в КП
3. Высшая КП.
В высшей паре два относительных движения - скольжение и перекатывание. Поэтому здесь имеют место два вида трения - трение скольжения и трение качения (рис. 9.9).
При силовом расчете в высшей КП определяются:
величина реакции Fij ;
направление реакции Fij ;
момент сил трения Мтрij
известны:
точка приложения силы - точка контакта рабочих профилей кинематической пары С2вп;
направление нормальной составляющей Fnij - контактная нормаль к профилям (размеры и форма профилей заданы);
направление тангенциальной составляющей Fтрij - касательная к профилям в точке контакта;
коэффициенты трения качения k и скольжения f.
Полная величина реакции в КП равна векторной сумме
Число неизвестных в высшей КП при силовом расчете с учетом трения увеличилось с ns = 1 до ns = 3 ( так как в паре имеется два вида трения).
Силовой расчет механизмов с учетом сил трения.
Постановка задачи силового расчета: для исследуемого механизма при известных кинематических характеристиках и внешних силах, а также размерах элементов КП и величинах коэффициентов трения в них, определить уравновешивающую силу или момент (управляющее силовое воздействие) и реакции в кинематических парах механизма.
Методы решения задач силового расчета с учетом трения :
составление общей системы уравнений кинетостатики с уравнениями для расчета сил и моментов сил трения с числом уравнений соответствующим числу неизвестных;
метод последовательных приближений: на первом этапе решается задача кинетостатического расчета без учета трения и определяются нормальные составляющие реакций, по ним рассчитываются силы трения и определяются реакции с учетом трения.
Примечание: силовой расчет с учетом сил трения можно проводить на тех этапах проектирования, когда уже определены размеры элементов КП, материалы звеньев, образующих пары, классы чистоты рабочих поверхностей КП, вид смазки и скорости относительных движений, т.е. параметры по которым можно определить коэффициенты трения. Подробнее с силовым расчетом механизмов с учетом трения можно познакомится в учебнике [ 9.1 ] и в пособии [ 9.5 ].
Понятие о КПД механической системы.
Коэффициентом полезного действия или КПД механической системы называют отношение работы сил полезного сопротивления к работе движущих сил за цикл ( или целое число циклов ) установившегося режима работы.
КПД механизма характеризует его эффективность при преобразовании энергии, определяет соотношение полученной на выходе полезной энергии и энергетических потерь в механизме на трение, перемешивание масла, вентиляцию, деформацию звеньев и др. Величину КПД можно рассчитать по следующей зависимости:

h = 1 - | Aпот/ Ai | = 1 - y ,
где Ai - работа движущих сил, Aj - работа сил полезного сопротивления, h
- коэффициент полезного действия, y - коэффициент потерь.
Работа движущих сил за цикл


j
in ,j
jn и j
i0 , j
j0 - значения угловых координат звеньев i и j ,соответственно в начале и в конце цикла.
Подставим эти выражения в формулу для КПД и получим
h
= | Aj /Ai | = | Мcср *D
j
j | / | Мдср*D j
i | = | Мcср | / | Мдср | ,
где uji - передаточное отношение механизма.
КПД механической системы при последовательном и параллельном соединении механизмов.
при последовательном соединении (рис. 9.11) весь поток механической энергии проходит последовательно через каждый из механизмов

Литература к лекции 9:
1. Теория механизмов и машин. Под ред. К.В.Фролова. М.: Высшая школа, 1987.
Левитский Н.И. Колебания в машинах: Учебное пособие для втузов. - М: Наука. Гл. ред. физ. - мат. лит., 1988. - 336 с.
Штейнвольф Л.И. Динамические расчеты машин и механизмов. - Москва - Киев: Машгиз., 1961. - 340 с.
Вибрации в технике: Справочник. В 6-ти т./ Ред. совет: В.Н.Челомей и др.,- М.: Машиностроение, 1981. - Т.6, Защита от вибрации и ударов/ Под ред. К.В.Фролова, 1981. - 456с.
Силовой расчет, уравновешивание, проектирование механизмов и механика манипуляторов: Учебное пособие. Под ред. А.К.Мусатова. М.: Изд. МГТУ, 1990.
Волновые передачи
Краткое содержание:
[Назначение и области применения]
[Преимущества и недостатки волновых передач]
[Классификация типовых структурных схем ВЗП]
[Структура волновой зубчатой передачи]
[Кинематика волнового механизма]
[Расчет геометрии волнового зубчатого зацепления]
Волновые передачи:
Назначение и области применения:
Волновой передачей называется зубчатый или фрикционный механизм, предназначенный для передачи и преобразования движения (обычно вращательного), в котором движение преобразуется за счет волновой деформации венца гибкого колеса специальным звеном (узлом) – генератором волн. Основными элементами дифференциального волнового механизма являются: входной или быстроходный вал с генератором волн, гибкое колесо с муфтой, соединяющей его с первым тихоходным валом, жесткое колесо, соединенное со вторым тихоходным валом, корпус.
Рис. 18.1

Существует большое количество конструкций волновых механизмов. Обычно эти механизмы преобразуют входное вращательное движение в выходное вращательное или поступательное. Волновые механизмы можно рассматривать как одну из разновидностей многопоточных планетарных механизмов, так как они обладают многозонным, а в случае зубчатого механизма, и многопарным контактом выходного звена с гибким колесом. Многозонный контакт обеспечивается за счет формы генератора волн (кулачок чаще с двумя, редко с тремя выступами), многопарный – за счет податливости зубчатого венца гибкого колеса. Такое сочетание позволяет волновым механизмам передавать значительные нагрузки при малых габаритах. Податливость зубчатого венца обеспечивает достаточно равномерное распределение нагрузки по зубьям, находящимся в зоне зацепления. При номинальных нагрузках процент зубьев находящихся в зацеплении составляет 15-25% от общего их числа. Поэтому в волновых передачах применяется мелкомодульное зацепление, а числа зубьев колес лежат в пределах от 100 до 600. Зона зацепления в волновой зубчатой передаче совпадает с вершиной волны деформации.
По числу зон или волн передачи делятся на одноволновые, двухволновые и так далее. Передачи с числом волн более трех применяются редко. Распределение передаваемых усилий по нескольким зонам уменьшает нагрузку на элементы пар и позволяет существенно уменьшать габаритные размеры и массу механизмов. Многозонный и многопарный контакт звеньев существенно увеличивает жесткость механизма, а за счет осреднения ошибок и зазоров, уменьшает мертвый ход и кинематическую погрешность механизма. Поэтому волновые механизмы обладают высокой кинематической точностью и, несмотря на наличие гибкого элемента, достаточно высокой жесткостью. Образующиеся в структуре волнового механизма внутренние контуры, увеличивают теоретическое число избыточных или пассивных связей в механизме. Однако гибкое колесо за счет податливости компенсирует ряд возникающих перекосов. Поэтому при изготовлении и сборке волновых механизмов число необходимых компенсационных развязок меньше чем в аналогичных механизмах с жесткими звеньями. Гибкое колесо обеспечивает волновым передачам возможность передачи движения через герметичную стенку, которая разделяет две среды (например, космический аппарат и открытый космос). При этом гибкое колесо выполняется как элемент герметичной стенки, входной вал и генератор волн располагаются по одну сторону стенки (внутри космического аппарата), а выходное звено – по другую (в космическом пространстве). Схема герметичной волновой передачи приведена на рис. 18.2.
Рис. 18.2

Волновая передача не может рассматриваться в рамках ранее принятых нами допущений, так как в ней содержится гибкое звено. Поэтому необходимо определить место гибкого элемента в структуре механизма. Гибкая связь обычно допускает по действием силовых воздействий определенные относительные перемещения соединяемых звеньев. Поэтому ее отнесем к отношениям между элементами или к упругой кинематической паре. Зубчатое колесо представляет собой замкнутую систему зубьев. В каждый рассматриваемый момент в контакте в высшей паре могут находится один или несколько зубьев. Так как зубчатые колеса – звенья, то зубья – элементы высшей кинематической пары. Поэтому многопарный контакт между зубчатыми колесами является контактом между элементами одной кинематической пары. Пассивные или избыточные связи, возникающие в этом контакте, относятся к внутренним связям кинематической пары и в структурном анализе на уровне звеньев не учитываются. Поэтому считаем, что в зацеплении находится один зуб. Структурная схема механизма с остановленным жестким колесом при гибком соединении зуба с валом гибкого колеса может быть представлена следующем образом.
Рис. 18.3
Волновая зубчатая передача с упругой муфтой – стаканом.
|
Рис. 18.4
Волновая зубчатая передача с волновой зубчатой муфтой.
|
Рассмотрим звенья и кинематические пары механизмов:
звенья: 0 - корпус с закрепленным на нем жестким колесом.
1 - быстроходный вал с генератором волн.
2 - зуб гибкого колеса.
3 - вал гибкого колеса.
кинематические пары: А1ви Е1в - одноподвижные вращательные пары.
В2н– двухподвижная низшая пара (рис.18.5). Эта пара образована зубом гибкого колеса и кулачком генератора волн. Пара допускает два независимых движения зуба относительно кулачка: по касательной к профилю кулачка (по оси х) и в осевом направлении (по оси у). Вращение зуба вокруг оси у и перемещения его по оси z не являются независимыми и определяются формой профиля кулачка.
D3упр– двухподвижный упругий шарнир (рис.18.6).
Данная кинематическая пара должна обеспечивать зубу гибкого колеса 2 возможность выполнять движения деформации относительно вала 3, но относительные движения в тангенциальном направлении (по оси х) запрещены. Аналогичные движения обеспечивает пара D3муф в зубчатом соединении в волновой зубчатой муфте и пара С3вп в волновом зубчатом зацеплении (рис.18.7). Оси координат в зубчатой паре направляются так:
ось z - по касательной к профилям в точке контакта, ось х – по нормали к профилям и ось у – по линии контакта зубьев.
Рис. 18.7
Подвижность механизма подсчитывается следующим образом: n = 3, p1 = 2, p2 = 1, p3 = 2.
Wпр = 6Ч 3 - 5Ч 2 - 4Ч 1 - 3Ч 2 = 18 – 20 = -2. В механизме имеется одна местная подвижность Wм= 1 – подвижность зуба гибкого колеса в осевом направлении (по оси у).
Заданная или основная подвижность механизма W0= 1. Число избыточных связей в механизме равно:
qпр = W0 + Wм + Wпр = 1+1- (-2) = 4. Эти избыточные или пассивные связи определяют требование параллельности осей пар В,С,D и Е оси пары А. Движение всех звеньев волнового механизма осуществляется в параллельных плоскостях. Поэтому механизм волновой зубчатой передачи можно рассматривать как плоский. В этом случае:
n = 3; p1 = 3; p2 = 2;
Wпл = 3Ч 3 - 2Ч 3 - 1Ч 2 = 9 – 8 = 1.
Wм= 0; W0 = 1; qпл = W0 + Wм + Wпл = 1-1 = 0.
Классификация типовых структурных схем ВЗП: В таблице 18.1 приведены наиболее распространенные структурные схемы типовых волновых зубчатых передач, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях. Основное отличие одной схемы от другой заключается в конструкции муфты соединяющей гибкий зубчатый венец с корпусом или с выходным тихоходным валом. В таблице показаны только три наиболее распространенных разновидности: гибкая оболочка в форме стакана, гибкая труба с шлицевым соединением и волновая зубчатая муфта. Если в передаче с гибким колесом – кольцом (в третьей из рассматриваемых схем), второе волновое зацепление выполнить как волновую зубчатую передачу, то получим двухступечатую ВЗП.
Таблица 18.1
|
№ |
Структурная схема ВЗП |
uред |
h |
|
1. |
|
50… 300 uh1ж= -zг / (zж- zг) |
0.95 ...0.8 |
|
2. |
|
50… 300 uh1ж= -zг / (zж- zг) |
0.9 ...0.8 |
|
3. |
|
2000… 105 uh1ж = z1Чzг /
/ ( z1Чzг- zмЧzж) |
0.2..0.01 |
40… 300 Если zм= z1, то
uh1ж= -zг / (zж- zг) |
0.85..0.7 |
Кинематика волнового механизма:
Рассмотрим идеальную фрикционную волновую передачу. В этой передачи контактирующие поверхности гибкого и жесткого колес будут соответствовать начальным поверхностям зубчатых колес. Толщину гибкого колеса принимаем бесконечно малой. Тогда срединная поверхность гибкого колеса совпадает с его начальной поверхностью. Считаем, что срединная поверхность гибкого колеса нерастяжима, то есть длина ее до и после деформирования колеса генератором волн остается неизменной. Рис. 18.8
На рис.18.8 приняты следующие обозначения: rwу - радиус начальной окружности условного колеса;
rwж - радиус начальной окружности жесткого колеса;
rд - радиус деформирующего диска;
rсг - радиус срединной окружности гибкого колеса;
rсу - радиус срединной окружности условного колеса;
w0 - радиальная деформация гибкого колеса.
Рассмотрим движение звеньев дифференциального волнового механизма относительно генератора волн.
Тогда угловые скорости звеньев изменятся следующим образом:
Таблица 18.2
| Движение механизма |
Звено г |
Звено ж |
Звено h |
Звено 0 |
| относительно стойки |
wг |
wж |
wh |
w0=0 |
| относительно генератора волн |
w*г=wг-wh |
w*ж=wж-wh |
wh-wh=0 |
-wh |
В движении звеньев относительно генератора волн скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость генератора. Скорость точки жесткого колеса, совпадающей с полюсом зацепления VPж = (wж- wh) Чrwж,а скорость точки, совпадающей с полюсом на гибком колесе VPг = (wг- wh) Чrwг В полюсе зацепления нет скольжения и VPж = VPг, а так как срединную поверхность оболочки считаем нерастяжимой то VPг = VС . Тогда для движения относительно генератора волн VPж = (wж- wh) Ч rwж ; VС = (wг- wh) Ч rwг VPж = VС Ю (wж- wh) Ч rwж = (wг- wh) Ч rwг (wж- wh)/ (wг- wh) = rwг / rwж = zг / zж ,
| zж Ч wж + (zг – zж) Ч wh - zгЧ wг = 0. |
Для волнового зубчатого редуктора (1) :
при заторможенном жестком колесе wж= 0
| uhгж = wh / wг = - zг / (zж – zг) |
при заторможенном гибком колесе wг= 0
| uhжг = wh / wж = zж / (zж – zг) |
Расчет геометрии волнового зубчатого зацепления:
В расчете геометрии волнового зацепления существует два основных подхода. В первом методе (2) исследуется относительное движение зубьев и, на основе этого, разрабатываются рекомендации по выбору геометрических параметров зацепления. Второй метод (3) основан на использовании расчетного внутреннего зацепления жесткого колеса с условным расчетным колесом. Это колесо вписывается в деформированное гибкое колесо на участке возможного зацепления. Преимуществом первого метода можно считать относительную универсальность, которая позволяет в расчете геометрии учитывать деформации как гибкого, так и жесткого колеса под нагрузкой. Однако разработать рекомендации даже для небольшого количества конструкций ВЗП затруднительно. Второй метод позволяет использовать для расчета геометрии стандартный расчет внутреннего эвольвентного зацепления для пары колес zжи zу.
Число зубьев условного колеса рассчитывается по следующей формуле:
где: mw= w0 / rсг - относительная деформация гибкого колеса.
kb - коэффициент, определяемый углом b
b - угловая координата участка постоянной кривизны деформированной кривой гибкого колеса.После определения zy определяются:
толщина гибкого колеса под зубчатым венцом hc
hc = (60 + 0,2 Ч zг) Чm Чzг Ч10 –4
коэффициент смещения гибкого колеса
xг = (ha* + c* + 0,5 Чhc/m) Чd
относительная деформация
mw = w0 / rсг= ± [(zж – zг) / zг ] Чg,где при внутреннем деформировании: знак ( + ) , d = 1 , g = 0,95 …1.1
,а при внешнем деформировании: знак ( - ) , d= 0,8.. 0,9 , g = 0,85 …1.1
радиус срединной окружности условного колеса
rcy = ( zг + xг ± ha* ± c* ± 0,5 Чhc/m) Чm
радиус срединной окружности гибкого колеса
rcг = ( zг / zу ) Чrcy
межосевое расстояние
aw = ± rcг Ч( 1 + mw) + rcy
угол зацепления
aw = arccos [± (zж – zy) Чm Чcos a ] / (2 Чaw ).Далее расчет ведется по стандартному алгоритму расчета внутреннего эвольвентного зацепления (3).
Литература:
Гинзбург Е.Г. Волновые зубчатые передачи. – Л.: Машиностроение, 1969. – 159 с., ил. Волновые механические передачи. Методические рекомендации. – М.: НИИИ по Машиностроению, 1976. – 83 с., ил. Волновые зубчатые передачи. Роботы-манипуляторы. Конспект лекций. – М.: МГТУ им. Н.Э.Баумана, 1980. – 58 с., ил.
Цель и задачи курса ОПМ-ТММ
Краткое содержание: Введение. Цель и задачи курса ОПМ-ТММ. Краткая историческая справка. Место курса в системе подготовки инженера. Инженерное проектирование. Основные этапы процесса проектирования. Методы проектирования. Машинный агрегат и его составные части. Классификация машин. Механизм и его элементы. Классификация механизмов.
Введение.
Курс “Теория машин и механизмов” является первой частью общеинженерной дисциплины “Основы проектирования машин”. Вторая часть этой дисциплины называется “Детали машин” или “Основы конструирования машин”. На специальности, по которой Вы проходите подготовку, курс ТММ изучается в течение двух семестров и состоит из:
1-ый семестр. Курс лекций объемом 36 часов, практических занятий (включая два рубежных контроля) - 16 часов, лабораторного практикума - 16 часов. В разделе самостоятельная работа два домашних задания: 1-ое домашнее задание “Структурный и кинематический анализ рычажного механизма”; 2-ое домашнее задание “Кинетостатический силовой расчет рычажного механизма”. Семестр завершается дифференцированным зачетом с учетом рейтинга по домашним заданиям, рубежным контролям и лабораторным работам.
2-ой семестр. Курсовая работа (проект) с объемом 4 листа графической части и пояснительная записка на 30-50 рукописных (машинописных) страниц. Содержание листов курсовой работы: лист 1 - динамический анализ машинного агрегата, лист 2 - кинетостатический силовой расчет основного рычажного механизма, лист 3 -проектирование механизмов с зубчатыми передачами, лист 4 - проектирование кулачковых механизмов. Курсовая работа защищается комиссии из двух преподавателей, по ней проставляется дифференцированный зачет.
Рекомендуемая основная литература
Теория механизмов и машин. Под ред. К.В.Фролова. М.: Высшая школа, 1987. Попов С.А. Курсовое проектирование по теории механизмов и механике машин. - М.: Высшая школа, 1986. Артоболевкий И.И. Теория механизмов и машин. - М.: Наука, 1988. Левитский Н.И.
Теория механизмов и машин. - М.,: Наука, 1990.
Рекомендуемая дополнительная литература
Теория механизмов. Под ред. В.А.Гавриленко. М.: Высшая школа, 1973. Заблонский К.И. и др. Теория механизмов и машин. - Киев.: Выша школа, 1989.
Цель и задачи курса.
Теория механизмов и машин - научная дисциплина (или раздел науки), которая изучает строение (структуру), кинематику и динамику механизмов в связи с их анализом и синтезом.(И.И.Артоболевский)
Цель ТММ - анализ и синтез типовых механизмов и их систем.
Задачи ТММ: разработка общих методов исследования структуры, геометрии, кинематики и динамики типовых механизмов и их систем.
Типовыми механизмами будем называть простые механизмы, имеющие при различном функциональном назначении широкое применение в машинах, для которых разработаны типовые методы и алгоритмы синтеза и анализа.
Рассмотрим в качестве примера кривошипно-ползунный механизм. Этот механизм широко применяется в различных машинах: двигателях внутреннего сгорания, поршневых компрессорах и насосах, станках, ковочных машинах и прессах. В каждом варианте функционального назначения при проектировании необходимо учитывать специфические требования к механизму. Однако математические зависимости, описывающие структуру, геометрию, кинематику и динамику механизма при всех различных применениях будут практически одинаковыми. Главное или основное отличие ТММ от учебных дисциплин изучающих методы проектирования специальных машин в том, что ТММ основное внимание уделяет изучению методов синтеза и анализа, общих для данного вида механизма, независящих от его конкретного функционального назначения. Специальные дисциплины изучают проектирование только механизмов данного конкретного назначения, уделяя основное внимание специфическим требованиям. При этом широко используются и общие методы синтеза и анализ, которые изучаются в кусе ТММ.
Краткая историческая справка
Как самостоятельная научная дисциплина ТММ, подобно другим прикладным разделам науки, возникла в результате промышленной революции начало которой относится к 30-м годам XVIII века.
Однако машины существовали за долго до этой даты. Поэтому в истории развития ТММ можно условно выделить четыре периода:
1-й период до начала XIX века - период эмпирического машиностроения в течение которого изобретается большое количество простых машин и механизмов: подъемники, мельницы, камнедробилки, ткацкие и токарные станки, паровые машины (Леонардо да Винчи, Вейст, Ползунов, Уатт). Одновременно закладываются и основы теории: теорема о изменении кинетической энергии и механической работы, “золотое правило механики”, законы трения, понятие о передаточном отношении, основы геометрической теории циклоидального и эвольвентного зацепления ( Карно, Кулон, Амонтон, Кадано Дж., Ремер, Эйлер).
2-й период от начала до середины XIX века - период начала развития ТММ . В это время разрабатываются такие разделы как кинематическая геометрия механизмов (Савари, Шаль, Оливье), кинетостатика (Кариолис), расчет маховика (Понселе), классификация механизмов по функции преобразования движения (Монж, Лану) и другие разделы. Пишутся первые научные монографии по механике машин (Виллис, Бориньи), читаются первые курсы лекций по ТММ и издаются первые учебники (Бетанкур, Чижов, Вейсбах).
3-й период от второй половины XIX века до начала XX века - период фундаментального развития ТММ. За этот период разработаны: основы структурной теории (Чебышев, Грюблер, Сомов, Малышев), основы теории регулирования машин (Вышнеградский), основы теории гидродинамической смазки (Грюблер), основы аналитической теории зацепления (Оливье, Гохман), основы графоаналитической динамики (Виттенбауэр, Мерцалов), структурная классификация и структурный анализ (Ассур), метод планов скоростей и ускорений (Мор, Манке), правило проворачиваемости механизма (Грасгоф) и многие другие разделы ТММ.
4-й период от начала XX века до настоящего времени - период интенсивного развития всех направлений ТММ как в России, так и за рубежом. Среди русских ученых необходимо отметить обобщающие работы Артоболевского И.И., Левитского Н.И., Фролова К.В.; в области структуры механизмов - работы Малышева , Решетова Л.Н., Озола О.Г.; по кинематике механизмов - работы Колчина Н.И., Смирнова Л.П., Зиновьева В.А.; по геометрии зубчатых передач - работы Литвина Ф.Л., Кетова Х.Ф., Гавриленко В.А., Новикова М.Л.; по динамике машин и механизмов - Горячкин В.П., Кожевников С.Н., Коловский М.З.
и др. Данное перечисление не охватывает и малой доли работ выдающихся ученых, внесших существенный вклад в развитие ТММ в этот период. Из зарубежных ученых необходимо отметить работы Альта Х., Бегельзака Г., Бейера Р., Крауса Р., Кросли Ф. и многих других.
Основные разделы курса ТММ
структура механизмов и машин;
геометрия механизмов и их элементов;
кинематика механизмов;
динамика машин и механизмов.
Связь курса ТММ с общеобразовательными, общеинженерными и специальными дисциплинами.
Лекционный курс ТММ базируется на знаниях полученных студентом на младших курсах при изучении физики, высшей и прикладной математики, теоретической механики, инженерной графики и вычислительной техники. Знания, навыки и умение приобретенные студентом при изучении ТММ служат базой для курсов детали машин, подъемно-транспортные машины, системы автоматизированного проектирования, проектирование специальных машин и основы научных исследований.
Понятие о инженерном проектировании.
Инженерное проектирование - это процесс, в котором научная и техническая информация используется для создания новой системы, устройства или машины, приносящих обществу определенную пользу [ 7 ].
Проектирование (по ГОСТ 22487-77) - это процесс составления описания, необходимого для создания еще несуществующего объекта (алгоритма его функционирования или алгоритма процесса), путем преобразования первичного описания, оптимизации заданных характеристик объекта (или алгоритма его функционирования), устранения некорректности первичного описания и последовательного представления (при необходимости) описаний на различных языках.
Проект (от латинского projectus - брошенный вперед) - совокупность документов и описаний на различных языках (графическом - чертежи, схемы, диаграммы и графики; математическом - формулы и расчеты; инженерных терминов и понятий - тексты описаний, пояснительные записки), необходимая для создания какого-либо сооружения или изделия.
Методы проектирования.
Прямые аналитические методы синтеза (разработаны для ряда простых типовых механизмов);
Эвристические методы проектирования - решение задач проектирования на уровне изобретений (например, алгоритм решения изобретательских задач [8]);
Синтез методами анализа - перебор возможных решений по определенной стратегии (на пример, с помощью генератора случайных чисел – метод Монте-Карло) с проведением сравнительного анализа по совокупности качественных и эксплуатационных показателей (часто используются методы оптимизации - минимизация сформулированной разработчиком целевой функции, определяющей совокупность качественных характеристик изделия);
Системы автоматизированного проектирования или САПР - компьютерная программная среда моделирует объект проектирования и определяет его качественные показатели, после принятия решения - выбора проектировщиком параметров объекта, система в автоматизированном режиме выдает проектную документацию.
Другие методы проектирования [9, 10, 11].
Основные этапы процесса проектирования.
| 1. |
Осознание общественной потребности в разрабатываемом изделии |
| 2. |
Техническое задание на проектирование (первичное описание) |
| 3. |
Анализ существующих технических решений |
| 4. |
Разработка функциональной схемы |
| 5. |
Разработка структурной схемы |
| 6. |
Метрический синтез механизма (синтез кинематической схемы) |
| 7. |
Статический силовой расчет |
| 8. |
Эскизный проект |
| 9. |
Кинетостатический силовой расчет |
| 10. |
Силовой расчет с учетом трения |
| 11. |
Расчет и конструирование деталей и кинематических пар (прочностные расчеты, уравновешивание, балансировка, виброзащита) |
| 12. |
Технический проект |
| 13. |
Рабочий проект (разработка рабочих чертежей деталей, технологии изготовления и сборки) |
| 14. |
Изготовление опытных образцов |
| 15. |
Испытания опытных образцов |
| 16. |
Технологическая подготовка серийного производства |
| 17. |
Серийное производство изделия |
Понятие о технической системе и ее элементах.
(из теории технических систем по[11])
Техническая система - ограниченная область реальной действительности, взаимодействующая с окружающей средой U, выполняющая определенные функции F и имеющая структуру S.
Ef, Af - параметры, характеризующие функции F системы;
En An - параметры, не относящиеся к функциям прибора (условия работы, внешние и дополнительные воздействия);
Z - системный оператор;
M - элементы системы;
R - отношения между элементами системы.
Окружающая среда U - совокупность внешних объектов, взаимодействующих с системой.
Функция F - свойство системы, используемое для преобразования входных величин Ef, при внешних и дополнительных воздействиях An
и условиях работы En, в выходные величины Af. Функция является объективно измеряемое свойство, которое может быть охарактеризовано параметрами системы. Количество реализуемых системой функций соответствует количеству используемых системой физических свойств. Если система выполняет несколько функций, то различают общую и частные функции. Общая функция охватывает множество всех входных и выходных величин, которое характеризует рассматриваемую систему как одно целое. Частные функции делятся на: главные и вспомогательные - по их значению в выполнении задачи; основные и элементарные - по типу изменения изменений функций в процессе их выполнения.
Структура S - совокупность элементов М и отношений R между ними внутри системы S=(M,R). Элемент системы при проектировании рассматривается, как одно целое, хотя он может иметь различную степень сложности. Если при рассмотрении элемента, не принимается во внимание его форма и внутреннее строение, а рассматривается только выполняемая им функция, то такой элемент называется функциональным. Для механической системы элементами могут быть: деталь, звено, группа, узел, простой или типовой механизм. Деталь - элемент конструкции не имеющий в своем составе внутренних связей (состоящий из одного твердого тела). Звено - твердое тело или система жестко связанных твердых тел (может состоять из одной или нескольких деталей) входящая в состав механизма. Группа
- кинематическая цепь, состоящая из подвижных звеньев, связанных между собой кинематическими парами (отношениями), и удовлетворяющая некоторым заданным условиям. Узел - несколько деталей связанных между собой функционально, конструктивно или каким-либо другим образом.
С точки зрения системы узлы, группы, простые или типовые механизмы рассматриваются как подсистемы. Самым низким уровнем разбиения системы при конструировании является уровень деталей ; при проектировании - уровень звеньев. Элементы из системы можно выделить только после определения взаимосвязей между ними, которые описываются отношениями. Для механических систем интерес представляют отношения определяющие структуру системы и ее функции, т.е. расположения и связи. Расположения - такие отношения между элементами, которые описывают их геометрические относительные положения. Связи - отношения между элементами, предназначенные для передачи материала, энергии или информации между элементами. Связи могут осуществляться с помощью различных физических средств: механических соединений, жидкостей, электромагнитных или других полей, упругих элементов. Механические соединения могут быть подвижными(кинематические пары) и неподвижными. Неподвижные соединения делятся на разъемные (винтовые, штифтовые) и неразъемные (сварные, клеевые).
Машины и их классификация.
Машина - техническое устройство, выполняющее преобразование энергии, материалов и информации с целью облегчения физического и умственного труда человека, повышения его качества и производительности.
Существуют следующие виды машин:
1. Энергетические машины - преобразующие энергию одного вида в энергию другого вида. Эти машины бывают двух разновидностей:
Двигатели (рис.1.2), которые преобразуют любой вид энергии в механическую (например, электродвигатели преобразуют электрическую энергию, двигатели внутреннего сгорания преобразуют энергию расширения газов при сгорании в цилиндре).
Генераторы (рис.1.3), которые преобразуют механическую энергию в энергию другого вида (например, электрогенератор преобразует механическую энергию паровой или гидравлической турбины в электрическую).
2. Рабочие машины - машины использующие механическую энергию для совершения работы по перемещению и преобразованию материалов.
Эти машины тоже имеют две разновидности:
Транспортные машины (рис.1.4), которые используют механическую энергию для изменения положения объекта (его координат).
Технологические машины (рис.1.5), использующие механическую энергию для преобразования формы, свойств, размеров и состояния объекта.
3. Информационные машины - машины, предназначенные для обработки и преобразования информации. Они подразделяются на:
Математические машины (рис.1.6), преобразующие входную информацию в математическую модель исследуемого объекта.
Контрольно-управляющие машины (рис.1.7), преобразующие входную информацию (программу) в сигналы управления рабочей или энергетической машиной.
4. Кибернетические машины (рис.1.8) - машины управляющие рабочими или энергетическими машинами, которые способны изменять программу своих действий в зависимости от состояния окружающей среды (т.е. машины обладающие элементами искусственного интеллекта).
Понятие о машинном агрегате.
Машинным агрегатом называется техническая система, состоящая из одной или нескольких соединенных последовательно или параллельно машин и предназначенная для выполнения каких-либо требуемых функций. Обычно в состав машинного агрегата входят : двигатель, передаточный механизм и рабочая или энергетическая машина. В настоящее время в состав машинного агрегата часто включается контрольно-управляющая или кибернетическая машина. Передаточный механизм в машинном агрегате необходим для согласования механических характеристик двигателя с механическими характеристиками рабочей или энергетической машины.
Схема машинного агрегата.
Механизм и его элементы.
В учебной литературе используются несколько определений механизма:
Первое: Механизмом называется система твердых тел, предназначенная для передачи и преобразования заданного движения одного или нескольких тел в требуемые движения других твердых тел [4, 12].
Второе: Механизм - кинематическая цепь, в состав которой входит неподвижное звено (стойка) и число степеней свободы которой равно числу обобщенных координат, характеризующих положение цепи относительно стойки [1, 3, 5, 6].
Третье: Механизмом называется устройство для передачи и преобразования движений и энергий любого рода [13].
Четвертое: Механизм - система твердых тел, подвижно связанных путем соприкосновения и движущихся определенным, требуемым образом относительно одного из них, принятого за неподвижное [14].
В этих определениях использованы раннее не определенные понятия:
Звено - твердое тело или система жестко связанных тел, входящих в состав механизма. Кинематическая цепь - система звеньев, образующих между собой кинематические пары. Кинематическая пара - подвижное соединение двух звеньев, допускающее их определенное относительное движение. Стойка - звено, которое при исследовании механизма принимается за неподвижное. Число степеней свободы или подвижность механизма - число независимых обобщенных координат однозначно определяющее положение всех его звеньев на плоскости или в пространстве.
Из теоретической механики: Системы материальных тел (точек), положения и движения которых подчинены некоторым геометрическим или кинематическим ограничениям, заданным наперед и не зависящим от начальных условий и заданных сил, называется несвободной. Эти ограничения наложенные на систему и делающие ее несвободной называются связями. Положения точек системы допускаемые наложенными на нее связями называются возможными. Независимые друг от друга величины q1,q2, ... qn, вполне и однозначно определяющие возможные положения системы в произвольный момент времени называются обобщенными координатами системы.
Недостатками этих определений являются: первое не отражает способности механизма преобразовывать не только движение, но и силы; второе не содержит указания выполняемой механизмом функции. Оба определения входят в противоречия с определением технической системы. Учитывая сказанное, дадим следующую формулировку понятия механизм:
Механизмом называется система, состоящая из звеньев и кинематических пар, образующих замкнутые или разомкнутые цепи, которая предназначена для передачи и преобразования перемещений входных звеньев и приложенных к ним сил в требуемые перемещения и силы на выходных звеньях.
Здесь: входные звенья - звенья, которым сообщается заданное движение и соответствующие силовые факторы (силы или моменты); выходные звенья
- те, на которых получают требуемое движение и силы.
Начальное звено - звено, координата которого принята за обобщенную. Начальная кинематическая пара - пара, относительное положение звеньев в которой принято за обобщенную координату.
Классификация механизмов.
Механизмы классифицируются по следующим признакам:
По области применения и функциональному назначению:
механизмы летательных аппаратов;
механизмы станков;
механизмы кузнечных машин и прессов;
механизмы двигателей внутреннего сгорания;
механизмы промышленных роботов (манипулятороы);
механизмы компрессоров;
механизмы насосов и т.д.
по виду передаточной функции на механизмы:
с постоянной передаточной функцией;
с переменной передаточной функцией:
с нерегулируемой (синусные, тангенсные);
с регулируемой:
со ступенчатым регулированием (коробки передач);
с бесступенчатым регулированием (вариаторы).
по виду преобразования движения на механизмы преобразующие :
вращательное во вращательное:
редукторы wвх > wвых;
мультипликаторы wвх < wвых;
муфты wвх = wвых;
вращательное в поступательное;
поступательное во вращательное;
поступательное в поступательное.
по движению и расположению звеньев в пространстве:
пространственные;
плоские;
сферические.
Все механизмы являются пространственными механизмами, часть механизмов, звенья которых совершают движение в плоскостях параллельных одной плоскости, являются одновременно и плоскими, другая часть механизмов, звенья которых движутся по сферическим поверхностям экивидистантным какой-либо одной сфере, являются одновременно и сферическими.
по изменяемости структуры механизма на механизмы:
с неизменяемой структурой;
с изменяемой структурой.
В процессе работы кривошипно-ползунного механизма насоса его структурная схема все время остается неизменной. В механизмах манипуляторов в процессе работы структурная схема механизма может изменяться.
Так если промышленный робот выполняет сборочные операции , например, вставляет цилиндрическую деталь в отверстие, то при транспортировке детали его манипулятор является механизмом с открытой или разомкнутой кинематической цепью. В тот момент когда деталь вставлена в отверстие, кинематическая цепь замыкается , структура механизма изменяется, подвижность уменьшается на число связей во вновь образованной кинематической паре деталь-стойка.
Структура манипулятора изменяется и тогда, когда в одной или нескольких кинематических парах включается тормоз. Тогда подвижное соединение двух звеньев заменяется неподвижным, два звена преобразуются в одно. На рис. 1.13 тормоз включен в паре С.
по числу подвижностей механизма:
с одной подвижностью W=1;
с несколькими подвижностями W>1:
суммирующие (интегральные);
разделяющие (дифференциальные).
по виду кинематических пар (КП):
с низшими КП ( все КП механизма низшие );
с высшими КП ( хотя бы одна КП высшая );
шарнирные (все КП механизма вращательные - шарниры).
по способу передачи и преобразования потока энергии:
фрикционные ( сцепления );
зацеплением;
волновые (создание волновой деформации);
импульсные.
по форме, конструктивному исполнению и движению звеньев:
рычажные ( рис.1.14);
зубчатые ( рис.1.15);
кулачковые ( рис. 1.16);
планетарные ( рис. 1.17);
манипуляторы ( рис.1.11-1.12).
|
|
| Рис.1.14 | Рис.1.15 |
|
|
| Рис.1.16 | Рис.1.17 |
Список дополнительной литературы к Лекции 1.
П.Хилл Наука и искусство проектирования. Методы проектирования, научное обоснование решений. Пер. с англ., Под ред. Венды В.Ф., М.: Мир, 1973.
Альтшуллер Г.С. Алгоритм изобретения. М.: Московский рабочий, 1973.
Джонс Дж. К. Методы проектирования. / Пер. с англ. 2-е изд. М.: Мир. 1986.
Дитрих Я. Проектирование и конструирование: Системный подход. Пер. с польск. - М.: Мир, 1981.
Конструирование приборов. В 2-х книгах. / Под ред. В.Краузе. - М.: Машиностроение. 1987.
Крайнев А.Ф. Словарь-справочник по механизмам. - М.: Машиностроение. 1981.
Р.Бейер Кинематический синтез механизмов: Основы теории метрического синтеза плоских механизмов. / Пер.с нем. М.: Машгиз. 1959.
Теория механизмов и механика машин. Под ред. К.В.Фролова. М.: Высшая школа, 1998.
Введение в теорию высшей пары
Краткое содержание: Введение в теорию высшей пары, основные понятия и определения. Механизмы с высшими кинематическими парами и их классификация. Передачи сцеплением и зацеплением. Основная теорема зацепления. Понятие о полюсе и центроидах. Сопряженные профили в высшей КП. Следствия основной теоремы зацепления. Первое следствие: скорость скольжения профилей в высшей КП. Второе следствие: центр вращения ведущего звена. Угол давления в механизмах с высшими КП. Зубчатые передачи и их классификация. Эвольвентная зубчатая передача. Эвольвента окружности и ее параметрические уравнения. Эвольвентное зацепление и его свойства.
Введение в теорию высшей пары, основные понятия и определения.
Два твердых тела (звена), соприкасающиеся своими поверхностями и имеющие возможность двигаться относительно друг друга, образуют кинематическую пару. Кинематическая пара допускает не любое движение звеньев относительно друг друга, а только такое движение, которое согласуется с характером соприкосновения и с формой соприкасающихся поверхностей.
Если звенья, образующие КП, в силу характера их соприкосновения, могут совершать только простейшие движения относительно друг друга ( вращательное, прямолинейное поступательное или, в общем случае, винтовое ), то пара является низшей. Низшая пара - пара, в которой требуемое относительное движение звеньев обеспечивается соприкасанием ее элементов по поверхности ( фактическое соприкасание звеньев в низшей паре возможно как по поверхности, так и по линиям и точкам ). В таких парах движение одного звена относительно другого представляет собой чистое скольжение, причем может иметь место поверхностный контакт - соприкасание звеньев по плоскости, цилиндрической или винтовой поверхности. Такая поверхность контакта может двигаться, “как бы оставаясь в самой себе”.
Более сложные относительные движения можно реализовать в парах, характер соприкасания звеньев в которых допускает не только относительное скольжение, но и перекатывание.
Такие пары называются высшими. Высшая пара - пара, в которой требуемое относительное движение звеньев может быть получено только соприкасанием звеньев по линиям или в точках. В высшей паре поверхностный контакт невозможен, так как он исключает возможность перекатывания тел. Если контакт в высшей КП происходит по линии, то она называется мгновенной контактной линией. Эта линия может быть прямой или кривой, при движении соприкасающихся тел она не только меняет свое положение по отношению к звеньям и к неподвижному пространству, но может менять и свою форму. Двигаясь относительно каждого из соприкасающихся звеньев, эта линия как бы “покрывает”, описывает или формирует его поверхность. То есть поверхность каждого из звеньев пары можно рассматривать как геометрическое место мгновенных контактных линий в системе координат, связанной со звеном. В неподвижном пространстве эти линии описывают поверхность зацепления - геометрическое место мгновенных контактных линий в неподвижной системе координат. Очевидно, что мгновенная контактная линия - линия пересечения поверхности зацепления с любой из двух соприкасающихся поверхностей. При точечном контакте, контактная точка в системах координат связанных со звеньями описывает некоторую контактную линию на контактирующей поверхности, в неподвижной системе координат - линию зацепления.
Как следует из вышеизложенного, характер относительного движения звеньев КП и геометрия их контактирующих поверхностей находятся в тесной взаимосвязи. Изучение геометрии контактирующих поверхностей в связи с их относительным движением составляет предмет раздела прикладной механики, который называется теорией зацепления [ 1, 2 ].
Механизмы с высшими кинематическими парами и их классификация.
К механизмам с высшими КП относятся любые механизмы в состав которых входит хотя бы одна высшая пара. Простейший типовой механизм с высшей парой состоит из двух подвижных звеньев, образующих между собой высшую кинематическую пару, а со стойкой низшие ( вращательные или поступательные ) пары.
К простейшим механизмам с высшей парой относятся :
фрикционные передачи (рис. 11.3), зубчатые передачи (рис. 11.2), кулачковые механизмы (рис. 11.1), поводковые механизмы (в том числе и мальтийские - рис. 11.4).
Структурные схемы простейших механизмов с высшими КП..
Фрикционными механизмами или передачами сцепления называются механизмы с высшей парой в которых передача движения в высшей паре осуществляется за счет сил сцепления или трения в зоне контакта. Кулачковым механизмом называется механизм с высшей парой, ведущее звено которого выполнено в форме замкнутой криволинейной поверхности и называется кулачком (или кулаком). Зубчатыми механизмами называются механизмы звенья которых снабжены зубьями (зубчатый механизм можно определить как многократный кулачковый, рассматривая зацепление каждой пары зубьев, как зацепление двух кулачков) . Рабочие поверхности зубьев должны быть выполнены так, чтобы обеспечивать передачу и преобразование движения по заданному закону за счет их зацепления . Условия, которым должны удовлетворять рабочие поверхности высших пар, формулируются в разделе теории механизмов - теории зацепления или теории высшей пары.
Основы теории высшей кинематической пары.
Основная теорема зацепления.
Понятие о полюсе и центроидах. Рассмотрим два твердых тела i и j, которые совершают друг по отношению к другу плоское движение. Свяжем с телом i систему координат 0i xiyi , а с телом j систему координат 0jxjyj . Плоское движение тела i относительно тела j в рассматриваемый момент эквивалентно вращению вокруг мгновенного центра скоростей или полюса P. Тогда геометрическое место полюсов относительного вращения в системе координат 0ixiyi называется подвижной Цi, а в системе координат 0jxjyj неподвижной Цjцентроидой. В процессе рассматриваемого движения цетроиды контактируют друг с другом в полюсах относительного вращения и поэтому перекатываются друг по другу без скольжения, т.е.
VPi = VPj ; VPiPj = 0 ;
тогда дуга Swi равна дуге Swj .
Полюс зацепления - мгновенный центр относительного вращения звеньев, образующих кинематическую пару.
Центроида (полоида) - геометрическое место центров (полюсов) относительного вращения в системах координат, связанных со звеньями.
Передаточное отношение для тел совершающих вращательное движение.
Рассмотрим два тела 1 и 2 , совершающих вращательное движение соответственно вокруг центров 01 и 02 с угловыми скоростями w 1 и w 2 (рис. 11.6). Причем нам неизвестно связаны эти тела между собой или нет. Как отмечено выше, полюс относительного вращения этих тел будет лежать в такой общей точке этих тел , где вектора скоростей как первого, так и второго тела будут равны. Для скоростей любой точки первого тела VA = w1*lA01 , для любой точки второго - VВ = w 2*lВ02 . Равенство векторов скоростей по направлению для тел, совершающих вращательное движение, возможно только на линии соединяющей центры вращения тел. Поэтому полюс относительного вращения должен лежать на этой линии. Для определения положения полюса на линии центров составим следующее уравнение
VP1 = w1 *l01P = w 1 * rw1,
VP2 = w2 *l02P = w 2 *rw2,
VP1 = VP2 , w1*rw1 = w 2 *rw2
u12 = w1/w2 = ± (rw2/rw1).
Таким образом, полюс относительного вращения звеньев лежит на линии центров и делит ее на отрезки обратно пропорциональные угловым скоростям.
Теорема Виллиса. Передаточное отношение между звеньями совершающими вращательное движение прямопропорционально отношению угловых скоростей и обратно пропорционально отношению расстояний от центров вращения до полюса.
Знак перед отношением показывает внешним (знак +, зацепление внутреннее) или внутренним (знак - , зацепление внешнее) образом делит полюс линию центров на отрезки rw1 = l 01P и rw2 = l 02P . Данная формула получена из рассмотрения вращательного движения двух тел, при этом тела могут быть и не связаны между собой.
Воспользуемся методом обращенного движения и рассмотрим движение нашей системы относительно звена 1. Для этого к скоростям всех звеньев механизма добавим - w 1. Тогда скорости звеньев изменятся следующим образом:
| Движение механизма: |
Звено 1 |
Звено 2 |
Звено 0 |
| исходное |
w 1 |
w 2 |
w 0 = 0 |
| относительно звена 1 |
w 1 - w1 = 0 |
w 21 = w2 - w 1 |
w 1 = - w01 |
Скорость любой точки звена 2 в относительном движении будет равно его угловой скорости в этом движении умноженной на расстояние от этой точки до полюса относительного вращения, т.
е.
VO2 = w21*l 02P = (w2 - w1) *rw2 .
Перейдем к рассмотрению двух тел 1 и 2 , совершающих вращательное движение, соответственно вокруг центров 01и 02 с угловыми скоростями w 1 иw2 , и образующих между собой высшую кинематическую пару К (рис. 11.7).
Условием существования высшей кинематической пары является условие неразрывности контакта звеньев, которое заключается в том, что проекции скоростей звеньев в точке контакта на контактную нормаль к профилям должны быть равны
Vпр. n-nK1 = Vпр.n-nK2 или VK2K1* n = 0,
т.е. скалярное произведение вектора относительной скорости в точке контакта на орт нормали равно нулю. Это условие обеспечивается, если скорость относительного движения контактных точек лежит на касательной ( в пространстве в касательной плоскости ). При выполнении этого условия профили не отстают друг от друга ( нарушение контакта приведет к исчезновению пары ), и не внедряются друг в друга
( что при принятом допущении о абсолютно жестких звеньях, невозможно ).
Как было показано выше скорость относительного скольжения в точке контакта равна
VK2K1 = w21 * lKP ,
где lKP - расстояние от контактной точки до полюса относительного вращения. Так как VK2K1 перпендикулярна lKP >, а VK2K1 должна лежать на касательной, то lKP является нормалью к профилям в точке контакта. То есть контактная нормаль к профилям в высшей паре пересекает линию центров в полюсе относительного вращения.
Основная теорема зацепления.
Формулировка анализа. Контактная нормаль к профилям высшей пары пересекает линию центров в полюсе относительного вращения звеньев ( то что полюс делит линию центров на отрезки обратно пропроциональные угловым скоростям было доказано выше ).
Формулировка синтеза. Профили в высшей кинематической паре должны быть выполнены так, чтобы контактная нормаль к ним проходила через полюс относительного вращения звеньев.
Так как положение полюса на линии центров определяет передаточное отношение механизма, то профили удовлетворяющие основной теореме зацепления обеспечивают заданный закон изменения передаточного отношения или являются сопряженными.
Скорость скольжения в высшей КП или перовое следствие основной теоремы зацепления.
Скорость скольжения профилей в высшей КП равна произведению скорости относительного вращения на расстояние от контактной точки до полюса зацепления.
VK2K1 = w21 *l KP = (w2 ±w1) * l KP ,
где верхний знак относится к внешнему зацеплению, нижний - к внутреннему. Зацепление считается внешним, если полюс делит линию центров внутренним образом и направления угловых скоростей звеньев противоположны, и внутренним, если полюс делит линию центров внешним образом (Рис. 17.8) и направления угловых скоростей одинаковы.
Из формулы видно, что скорость скольжения во внутреннем зацеплении много меньше, чем во внешнем.
Определение центра вращения ведущего звена или второе следствие основной теоремы зацепления.
Из схемы, изображенной на рис. 11.7, видно, что
D Kk1k2 ? D K01D и VK2 / lKD = VK1 / l01K = w 1
или lKD = VK2 / w1 = VqK2 ,
т.е. отрезок lKD , отсекаемый от луча, проведенного из точки О2 через точку K, прямой параллельной контактной нормали, равен передаточной функции точки K2.
Второе следствие основной теоремы зацепления.
Формулировка синтеза. Если на продолжении луча, проведенного из точки О2 через точку K, отложить от точки K отрезок длиной lKD = VK2 / w1 = VqK2 и через конец этого отрезка провести прямую параллельную контактной нормали, то эта прямая пройдет через центр вращения ведущего звена точку О1 .
С использованием этого свойства механизма с высшей парой при проектировании кулачковых механизмов определяют радиус начальной шайбы по допустимому углу давления.
Формулировка анализа. Луч проведенный через центр вращения ведущего звена точку О2 параллельно контактной нормали, отсекает на луче проведенном из точки О2 через точку K отрезок lKD = VK2 / w1 = VqK2 , равный передаточной функции точки K2.
Угол давления в высшей паре ( на примере плоского кулачкового механизма ).
Рассмотрим плоский кулачковый механизм с поступательно движущимся роликовым толкателем ( Рис. 11.9).
Из D BPF
tg J = lFP / lKF ,
где
Подставляя эти выражения в формулу для тангенса угла давления, получим
где знак - соответствует смещению оси толкателя (эксцентриситету) вправо от центра вращения кулачка.
Формула Эйлера - Савари.
При синтезе плоских зацеплений широко применяется формула Эйлера-Савари, которая устанавливает связь между радиусами кривизны центроид и радиусами кривизны профилей высшей пары. Эта формула записывается так
(1/rw1) + (1/rw2) = {[1/(r1 - lKP)] + [1/(r2 - lKP)]}* cos j ,
где rw1 и rw2 - радиусы кривизны центроид первого и второго звена в полюсе зацепления, r 1 и r 2 - радиусы кривизны профилей в контактной точке, lKP - расстояние от полюса зацепления до контактной точки, j - угол между контактными нормалями к профилям и центроидам.
Теорема Оливье.
Теорема Оливье является основополагающей теоремой как для плоских, так и для пространственных зацеплений. Она устанавливает основные признаки определяющие свойства зацепляющихся поверхностей, вид их контакта друг с другом.
Теорема Оливье. Пусть F1 , F2 и B некоторые поверхности с определенным абсолютным движением. И пусть F1 и F2 огибающие к B в их относительном движении, где - мгновенные контактные линии. Если K1 -K1 и K2 -K2 имеют общие точки, то поверхности F1 и F2 :
находятся в точечном контакте, если K1 -K1 и K2 -K2 пересекаются в некоторой точке K; находятся в линейном контакте, если K1 -K1 и K2 -K2 сливаюся в одну линию, образуя K -K.
Теорема Оливье имеет три важных следствия:
Следствие 1. Если оба зубчатых колеса обработаны друг другом, т.е. первое колесо обработано инструментом режущие кромки которого копируют второе колесо, а второое - инструментом режущие кромки которого копируют первое, то эти колеса имеют взаимоогибаемые поверхности зубьев с линейным контактом поверхностей.
Следствие 2. Если оба колеса обработаны инструментами, образующими между собой конгруентную пару, то эти колеса имеют взаимоогибаемые поверхности зубьев с линейным контактом поверхностей.
Следствие 3. Если поверхность зацепления И1 инструмента 1 с колесам 1 и поверхность зацепления И2 инструмента 2 с колесам 2 совпадает с поверхностью зацепления колес 1 и 2, то зубья колес обработанных при таком условии будут иметь линейный контакт.
Зубчатые передачи и их классификация.
Зубчатыми передачами называются механизмы с высшими кинематическими парами в состав которых входят зубчатые колеса, рейки или секторы - звенья, снабженные профилироваными выступами или зубьями. Зубчатые передачи бывают простые и сложные. Простая зубчатая передача - трехзвенные механизм, состоящий из двух зубчатых колес и стойки, в котором зубчатые колеса образуют между собой высшую пару, со стойкой - низшие ( поступательные или вращательные ).
Простые зубчатые передачи классифицируются:
по виду передаточной функции (отношения)
с постоянным передаточным отношением; с переменным передаточным отношением;
по расположению осей в пространстве
с параллельными осями; с пересекающимися осями; с перекрещивающимися осями;
по форме профиля зуба
эвольвентным профилем; с циклоидальным профилем; с круговым профилем (передачи Новикова);
по форме линии зуба
с прямым зубом; косозубые; шевронные; с круговым зубом;
по форме начальных поверхностей
цилиндрические; коническое; гиперболоидные;
по форме и виду зубчатых колес
червячные; с некруглыми колесами; винтовые.
Эвольвентная зубчатая передача.
Эвольвентная зубчатая передача - цилиндрическая зубчатая передача, профили зубьев которой выполнены по эвольвенте окружности.
Эвольвента окружности и ее свойства.
Эволютой называется геометрическое место центров кривизны данной кривой. Данная кривая по отношению к эволюте называется эвольвентой. Согласно определению нормаль к эвольвенте ( на которой лежит центр кривизны ) является касательной к эволюте. Эвольвенты окружности описываются точками производящей прямой при ее перекатывании по окружности, которую называют основной.
Свойства эвольвенты окружности:
Форма эвольвенты окружности определяется только радиусом основной окружности rb. При rb ? ? эвольвента переходит в прямую линию.
Производящая прямая является нормалью к эвольвенте в рассматриваемой произвольной точке My. Отрезок нормали в произвольной точке эвольвенты lMyN = r равен радиусу ее кривизны и является касательной к основной окружности.
Эвольвента имеет две ветви и точку возврата М0, лежащую на основной окружности. Эвольвента не имеет точек внутри основной окружности.
Точки связанные с производящей прямой но не лежащие на ней при перекатывании описывают: точки расположенные выше производящей прямой W - укороченные эвольвенты, точки, расположенные ниже производящей прямой L - удлиненные эвольвенты.
Параметрические уравнения эвольвенты получим из схемы, изображенной на рис. 11.11 . Так как производящая прямая перекатывается по основной окружности без скольжения то дуга М0N равна отрезку NMy . Для дуги окружности
М0N = rb*( inv ay - ay ),
из треугольника D OMyN
NMy = rb * tg a y ,
ry = rb / cos a y.
Откуда
inv a y = tg ay - ay ,
ry = rb / cos a y ,
получим параметрические уравнения эвольвенты.
Эвольвентное зацепление и его свойства.
В зубчатой передаче контактирующие элементы двух профилей выполняются по эвольвентам окружности и образуют, так называемое эвольвентное зацепление. Это зацепление обладает рядом полезных свойств, которые и определяют широкое распространение эвольвентных зубчатых передач в современном машиностроении. Рассмотрим эти свойства.
Свойство 1. Передаточное отношение эвольвентного зацепления определяется только отношением радиусов основных окружностей и является величиной постоянной.
u12 = w1 /w2 = rw2 / rw1 = (rb2*cos aw )/ (rb1*cos aw ) = rb2 / rb1 = const.
Свойство 2. При изменении межосевого расстояния в эвольвентном зацеплении его передаточное отношение не изменяется.
u’12 = w1 /w2 = r’w2 / r’w1 = (rb2*cos a ’w )/ (rb1*cos a ’w ) = rb2 / rb1 = const.
u’12 = u12 = rb2 / rb1 = const
Свойство 3. При изменении межосевого расстояния в эаольвентном зацеплении величина произведения межосевого расстояния на косинус угла зацепления не изменяется.
rb1 + rb2 = rw1 * cos aw + rw2 * cos aw = aw * cos aw ,
rb1 + rb2 = r’w1 * cos a ’w + r’w2 * cos a ’w = a’w * cos a ’w ,
aw * cos aw = a’w * cos a ’w = const.
Свойство 4. За пределами отрезка линии зацепления N1N2 рассматриваемые ветви эвольвент не имеют общей нормали, т. е. профили выполненные по этим кривым будут не касаться, а пересекаться. Это явление называется интерференцией эвольвент или заклиниванием.
Литература.
В.А.Гавриленко . Зубчатые передачи в машиностроении (Теория эвольвентных зубчатых передач). М.: Машгиз - 1962, 530 стр., илл. Ф.Л.Литвин Теория зубчатых зацеплений. Изд. 2-е, перераб. и доп. М.: - Наука - 1968, 584 стр., илл.
Задачи динамики механизмов с учетом податливости звеньев
Краткое содержание: Задачи динамики механизмов с учетом податливости звеньев (с упругими связями). Виды механических колебаний. Динамические модели механизмов с упругими связями (условия и допущения). Двухмассовая модель привода с упругими связями. Определение закона движения динамической модели. Упругие вынужденные колебания в системе. Определение собственных частот колебаний системы. Определение форм колебаний. Моделирование динамических процессов в приводе с упругими связями (влияние жесткости звеньев привода на неравномерность движения, момент в приводе и динамическую ошибку).
Задачи динамики механизмов с учетом податливости звеньев.
Звенья реальных механизмов под действием сил и моментов деформируются. При этом точки или сечения этих звеньев имеют относительные перемещения, которые влияют на их закон движения. Динамические модели реальных механизмов, учитывающие податливость звеньев делятся на дискретные модели и модели с распределенными параметрами. Дискретные модели как более простые применяются чаще. В этих моделях инерционные параметры рассматриваются как сосредоточенные в точках или сечениях звена, а податливость звена представляется как упругая связь (упругая кинематическая пара) между этими массами или моментами инерции.
К основным задачам динамики механизмов с упругими звеньями можно отнести:
определение резонансных режимов работы механической системы и устранение их изменением ее динамических параметров;
снижение виброактивности системы, уровня возбуждаемых ей звуковых (и других) колебаний;
повышение динамической точности;
применения вибраций или колебаний для выполнения технологический операций;
другие задачи.
Эти задачи решаются на базе общих методов исследования динамики линейных и нелинейных механических систем. Каждая из рассматриваемых задач может быть сформулирована как прямая (задача анализа) или как обратная (задача синтеза). В прямых задачах динамики при известных динамических параметрах системы определяют закон ее движения и другие характеристики.
В обратных задачах (задачах синтеза системы) – по заданным параметрам закона движения, частотам или формам колебаний определяются динамические или конструктивные параметры системы – массы, жесткости, коэффициенты демпфирования, внешние силы и другое. Решение обратной задачи или задачи синтеза более сложно, так как часто она имеет множество допустимых решений, из которых необходимо выбрать оптимальное.
Виды механических колебаний.
Механическими колебаниями (или просто колебаниями) называется такое движение механической системы при котором обобщенные координаты и их производные изменяются во времени периодически возрастая или убывая.
Различают следующие виды механических колебаний:
свободные или собственные колебания – происходящие без переменного внешнего воздействия и поступления энергии извне;
периодические – при которых значения обобщенной координаты и ее производных циклически повторяются (если это условие не выполняется, то колебания апериодические);
вынужденные – вызываемые и поддерживаемые переменной во времени внешней силой;
параметрические – вызываемые изменением во времени динамических параметров системы ( жесткости, массы или момента инерции, демпфирования и др.);
автоколебания – стационарные колебания возбуждаемые и поддерживаемые за счет энергии поступающей от источника неколебательного характера, в которой поступление энергии регулируется движением самой системы;
другие виды колебаний.
Динамическая модель системы с упругими связями.
Динамическая модель- математическая модель, которая отражает изменение рассматриваемого явления во времени. При формировании модели некоторыми свойствами объекта пренебрегают (эти свойства называются допущениями), другие свойства сохраняют неизменными (эти свойства называются критериями адекватности модели исследуемому объекту). В данном случае критериями адекватности являются:
кинетические и потенциальные энергии, которыми обладают звенья и упругие элементы объекта, равны кинетической и потенциальной энергии соответствующих элементов модели;
работы внешних сил и моментов для объекта и модели равны;
звенья модели (без учета их деформации) должны двигаться с одной частотой или скоростью.
При формировании дискретной динамической модели принимаем следующие допущения:
деформация упругих связей линейна и подчиняется закону Гука;
инерционные свойства звеньев отображаются сосредоточенными в точках массами или сосредоточенными в сечении моментами инерции;
упругие связи между этими массами и моментами инерции считаем безинерционными;
влиянием нерезонансных частот при резонансе пренебрегаем;
потери энергии при деформации упругих связей не учитываем.
Двухмассовая модель привода с упругими связями.
Рассмотрим механическую систему (рис.21.1), состоящую из двигателя 1, редуктора и исполнительного устройства 2.
На рис.21.1 приняты следующие обозначения:
I1 и I2* - моменты инерции соответственно ротора двигателя и исполнительного устройства, с1 и с2* - крутильные жесткости соответственно входного и выходного валов, Мд и Мс - моменты движущих сил и сил сопротивления, угловые координаты: j1 - ротора двигателя, j1' - шестерни редуктора, j2' - колеса редуктора и j2* - исполнительного устройства.
Согласно принятым допущениям приведем движения всех подвижных звеньев системы к движению с частотой (или скоростью) вала двигателя. Для этого определим приведенные жесткости, моменты и моменты инерции. При этом жесткости приводятся из условия равенства потенциальных энергий деформации, моменты - из условия равенства работ, моменты инерции - из равенства кинетических энергий. Для нашего примера:
Передаточное отношение редуктора:
.
Теорема о изменении кинетической энергии:
,
где
- изменение кинетической энергии системы,
- изменение потенциальной энергии системы,
- работа внешних сил.
Приведенный момент инерции исполнительного устройства
.
Приведенная крутильная жесткость выходного вала
.
Приведенная угловая координата исполнительного устройства
.
Приведенный момент сопротивления на валу исполнительного устройства
.
После приведения к одной частоте вращения расчетная схема динамической модели примет вид, изображенный на рис.21.2.
Два последовательно соединенных элемента системы можно заменить одним эквивалентным, при этом суммируются податливости этих элементов
, .
Окончательно расчетная схема принимает вид:
Определение закона движения динамической модели.
Положение звеньев динамической модели определяется двумя обобщенными координатами 

Разделим первое уравнение системы на I1, а второе - на I2, и получим:
Преобразуем уравнения системы следующим образом. Вычтем и первого уравнения (21.2) второе, а затем просуммируем уравнения (21.1). Тогда системы уравнений запишется в следующем виде:
Обозначим деформацию упругой связи . Ее вторая производная по времени
, откуда
. Обозначим также:
или
и
.
Подставим эти обозначения в (21.3) и получим:
Упругие вынужденные колебания в системе.
Первое уравнение системы содержит только координату деформации упругой связи
и описывает упругие колебания в системе, второе включает и координату связанную с движением системы без деформации
. Рассмотрим решение первого уравнения системы при следующих исходных данных:
,
.
С учетом этого первое уравнение системы (21.4) запишется так:
. (21.5)
Введем следующие обозначения
,
,
,
а также:
и
, и подставим в (21.5):
. (21.6)
Решение этого уравнения при
и начальных условиях
:
, (21.7)
| где: |
- свободные колебания с частотой p,
- гармонические колебания с частотой p и с амплитудой зависящей от ,
- вынужденные колебания с частотой возмущающей силы . |
Определение собственных частот колебаний системы.
Рассмотрим свободные колебания рассматриваемой системы, то есть положим
и
. Тогда система составленная из первого уравнения (21.4) и второго уравнения (21.3) запишется так:
Ищем решение этой системы в виде:
.
Для этого дифференцируем это выражение два раза:
и подставляем в систему (21.8):
,
.
Из первого уравнения если
, то
и
.
Из второго уравнения если
, то
и
. Нулевые частоты соответствуют движению системы без деформации.
Определение форм колебаний.
При деформации системы ее собственная частота не равна нулю
. Тогда
и
. Если принять
, то
и эпюра угловых координат по длине упругой связи будет иметь следующий вид:
При движении системы без деформации собственная частота колебаний равна нулю
. Тогда
,
и
. Эпюра угловых координат для движения без деформации показана на рис.21.5.
Пример для системы без упругих связей.
Если в рассмотренной модели принять с1 и с2
стремятся к бесконечности, то
стремится к
и
стремится к
. Расчетная схема этой динамической модели приведена на рис. 21.6, где:
|
IпрS - приведенный суммарный момент инерции
;
MпрS - приведенный суммарный момент внешних сил
;
DТ - изменение кинетической энергии
.
Уравнение движения для этой модели:
. |
Моделирование динамических процессов в приводе с упругими связями.
Рассмотренные выше уравнения движения механической системы можно использовать при моделировании поведения этой системы при различных значениях ее параметров. Ниже (на рис. 21.7) приведены результаты исследования влияния жесткости с на неравномерность вращения Dw, момент в приводе Мп и на динамическую ошибку y.
Задачи механики манипуляторов
Краткое содержание: Задачи механики манипуляторов. Кинематический анализ механизма манипулятора. Динамика манипуляторов промышленных роботов. Уравновешивание манипуляторов. Кинетостатический расчет манипуляторов. Расчет быстродействия привода.
Задачи механики манипуляторов.
К основным задачам механики манипуляторов можно отнести:
|
разработку методов синтеза и анализа исполнительных механизмов (включая механизмы приводов);
программирование движения манипулятора;
расчет управляющих усилий и реакций в КП;
уравновешивание механизмов манипуляторов;
другие задачи.
|
Эти задачи решаются на базе общих методов исследования структуры, геометрии, кинематики и динамики систем с пространственными многоподвижными механизмами. Каждая из рассматриваемых задач может быть сформулирована как прямая (задача анализа) или как обратная (задача синтеза). При определении функций положения механизма, в прямой задаче находят закон изменения абсолютных координат выходного звена по заданным законам изменения относительных или абсолютных координат звеньев. В обратной – по заданному закону движения схвата находят законы изменения координат звеньев, обычно, линейных или угловых перемещений в приводах. Решение обратной задачи или задачи синтеза более сложно, так как часто она имеет множество допустимых решений, из которых необходимо выбрать оптимальное. В обратной задаче кинематики по требуемому закону изменения скоростей и ускорений выходного звена определяются соответствующие законы изменения скоростей и ускорений в приводах манипулятора. Обратная задача динамики заключается в определении закона изменения управляющих сил и моментов в приводах, обеспечивающих заданный закон движения выходного звена.
Кинематический анализ механизма манипулятора.
Первая и основная задача кинематики – определение функции положения. Для пространственных механизмов наиболее эффективными методами решения этой задачи являются векторный метод и метод преобразования координат.
При решении прямой задачи о положении схвата манипулятора обычно используют метод преобразования координат. Из множества методов преобразования координат [ 1, 2 ] , которые отличаются друг от друга правилами выбора осей локальных систем координат, для манипуляторов обычно используется метод Денавита и Хартенберга.
Опишем два вида матриц:
матрицы М, определяющие отношение между системами координат соседних звеньев;
матрицы Т, определяющие положение и ориентацию каждого звена механизма в неподвижной или базовой системе координат.
Воспользуемся однородными координатами трехмерного проективного пространства РR3, в которых движение евклидова пространства R3 можно представить линейным преобразованием
где Мij – матрица 4x4 вида
.
Это преобразование эквивалентно преобразованию в эвклидовом пространстве
где
. То есть преобразованию, которое включает поворот, определяемый матрицей Uij размерностью 3х3, и параллельный перенос, задаваемый вектором
размерностью 3. В однородном пространстве положение точки будут определять не три x, y и z, а четыре величины x', y', z' и t', которые удовлетворяют следующим соотношениям:
x = x'/t', y = y'/t', z = z'/t'.
Обычно принимают t'=1. У матрицы поворота Uij
элементами uij являются направляющие косинусы углов между новой осью i
и старой осью j. Вектор
- трехмерный вектор, определяющий положение начала новой системы координат i в старой системе j. Выбор расположения осей должен соответствовать решаемой задаче. При решении задачи о положениях необходимо: в прямой задаче определить положение выходного звена как функцию перемещений в приводах, в обратной – заданное положение выходного звена представить как функцию перемещений в приводах. Выбор расположения и ориентации локальных систем координат должен обеспечивать выполнение этих задач. При использовании метода Денавита и Хартенберга оси координат располагаются по следующим правилам:
1. Для звена i ось zi направляется по оси кинематической пары, образуемой им со звеном ( i+1).
Начало координат размещают в геометрическом центре этой пары.
2. Ось xi направляется по общему перпендикуляру к осям zi-1 и zi с направлением от zi-1 к zi. Если оси zi-1 и zi совпадают, то xi
перпендикулярна к ним и направлена произвольно. Если они пересекаются в центре кинематической пары, то начало координат располагается в точке пересечения, а ось xi направляется по правилу векторного произведения
(кратчайший поворот оси zi до совмещения с zi-1 при наблюдении с конца xi должен происходить против часовой стрелки).
3. Ось yi направляется так, чтобы система координат была правой.
В прямой задаче необходимо определить положение схвата манипулятора и связанной с ним системы координат Mxnynzn по отношению к неподвижной или базовой системе координат Kx0y0z0. Это осуществляется последовательными переходами из системы координат звена i в систему координат звена i-1. Согласно принятому методу, каждый переход включает в себя последовательность четырех движений: двух поворотов и двух параллельных переносов, осуществляемых в указанной последовательности (см. рис. 20.1):
поворот i-ой системы вокруг оси xi на угол -qi до параллельности осей zi и zi-1 (положительное направление поворота при наблюдении с конца вектора xi против часовой стрелки);
перенос вдоль оси xi на величину -ai до совмещения начала системы координат Oi с точкой пересечения осей xi и zi-1 (отсчет по оси xi от точки пересечения оси xi и оси zi-1);
перенос вдоль оси zi-1 на величину -si, после которого начало системы координат Oi оказывается в начале координат Oi-1 системы (i-1) (отсчитывается по оси zi-1 от ее начала координат Oi-1 до точки ее пересечения с осью xi);
поворот вокруг оси zi-1 на угол -ji, до тех пор пока ось xi не станет параллельной оси xi-1 (положительное направление поворота при наблюдении с конца вектора zi-1 против часовой стрелки).
Необходимо отметить, что знак угла поворота не имеет значения, так как в матрицах перехода используются направляющие косинусы (четные функции).
Целесообразно рассматривать угол, обеспечивающий кратчайший поворот оси старой системы i до совмещения (параллельности) с соответствующей осью новой ( i-1). Перемещения начала координат определяются как координаты начала старой системы Oi в новой Oi-1.
В манипуляторах обычно используются одноподвижные кинематические пары или вращательные, или поступательные. Оба относительных движения как вращательное , так и поступательное, реализуются в цилиндрических парах. Поэтому при общем представлении механизма используются (рис.20.1) цилиндрические пары.
Матрицы перехода их системы Oi в систему Oi-1 можно записать так:
,
| где: |
|
- матрица поворота вокруг оси xiна угол -qi, |
|
|
- матрица переноса вдоль оси xi на -ai, |
|
|
- матрица переноса вдоль оси zi-1 на -si, |
|
|
- матрица поворота вокруг оси zi-1 на угол -ji. |
В этих матрицах переменные si и ji соответствуют относительным перемещениям звеньев в кинематических парах и являются обобщенными координатами манипулятора, определяющими конфигурацию механизма в рассматриваемом положении. Переменные ai и qi определяются конструктивным исполнением звеньев манипулятора, в процессе движения они остаются неизменными.
Положение некоторой произвольной точки М в системе координат звена i
определяется вектором rMi, а в системе координат звена (i-1) – вектором rMi-1. Эти радиусы связаны между собой через матрицу преобразования координат Мi следующим уравнением:
,
| где: |
|
- матрица перехода из i-ой системы координат в (i - 1)-ю. |
Рассмотрим шестиподвижный манипулятор в исходном или начальном положении (рис.20.2). За начальное положение принимается такое, в котором все относительные обобщенные координаты равны нулю. Переход из системы координат любого i–го звена к неподвижной или базовой системе записывается в виде
или
,
где
- матрица преобразования координат i–ой системы в координаты базовой системы координат.
Для схемы, изображенной на рис.20.2, радиус rM6 = 0, а радиус rM0 определится по формуле
,
то есть положение выходного звена манипулятора определяется матрицей Тn. Элементы этой матрицы определяют положение центра схвата точки М и ориентацию его в пространстве. Четвертый столбец определяет, декартовы координаты точки М (проекции вектора rM0на оси координат). Третий столбец содержит направляющие косинусы оси zn системы координат, связанной со схватом, или вектора подхода
, который характеризует направление губок схвата (рис.20.3). Второй столбец определяет направление оси yn или вектора ориентации
, который проходит через центр схвата по оси перпендикулярной рабочим поверхностям его губок. В первом столбце содержатся направляющие косинусы оси xn или вектора
. Углом подхода схвата
называется угол между вектором подхода
и базовым вектором
,
где
- орт вектора
неподвижной или базовой системы координат. С учетом сказанного, матрица Tnможет быть представлена в следующем виде
В результате матричных преобразований получаем радиус-вектор точки М схвата в функции обобщенных координат. Обычно, за обобщенные координаты принимают линейные и угловые перемещения в кинематических парах или на выходных валах приводов манипулятора. В механизме с n подвижностями в общем виде функцию положения схвата можно записать так
где q1, q2, … qn – обобщенные координаты манипулятора.
При кинематическом анализе манипулятора в прямой задаче необходимо определить линейные и угловые скорости и ускорения схвата при заданных угловых и линейных обобщенных скоростях и ускорениях (обычно относительных скоростях и ускорениях в кинематических парах механизма). В обратной задаче по заданному закону изменения скоростей и ускорений схвата определяются законы изменения скоростей и ускорений в КП или на выходных звеньях приводов. Решение прямой задачи кинематики для точки М схвата можно получить продифференцировав четвертый столбец матрицы Тn по времени
Угловую скорость и угловое ускорение схвата можно определить векторным суммированием относительных угловых скоростей во вращательных КП механизма.
Так как вектора угловых скоростей, при данном выборе ориентации осей координат, совпадают с осью z, то угловая скорость схвата
где
орт оси z системы координат, расположенной в центре КП, соединяющей звено i и звено i-1, m – число вращательных КП в механизме.
Дифференцируя это выражение по времени, получим формулу для определения углового ускорения схвата:
Динамика манипуляторов промышленных роботов.
Силовой расчет манипулятора.
Из большого разнообразия задач динамики манипуляторов рассмотрим две: силовой расчет и расчет быстродействия ПР. При силовом расчете манипуляторов решается задачи по определению внешних силовых управляющих воздействий, обеспечивающих требуемый закон движения механизма, и по расчету реакций в кинематических парах. Первую часть часто называют задачей синтеза управления . При силовом расчете обычно применяется метод кинетостатики, основанный на принципе Д’Аламбера. По этому методу к внешним силам и моментам, приложенным к звеньям механизма, добавляются расчетные силы инерции, которые обеспечивают силовую уравновешенность системы и позволяют рассматривать подвижную систему в квазистатическом равновесии, то есть, как условно неподвижную. Силовой расчет выполняется при заданной полезной нагрузке
, известных законах движения звеньев
и
(из предварительного кинематического расчета), известных инерционных характеристиках звеньев: массах звеньев mi и их моментах инерции Isi. По этим данным определяются главные вектора
и главные моменты
сил инерции для каждого из звеньев механизма. Для открытой кинематической цепи решение начинаем с выходного звена – схвата. Отброшенные связи звена n со звеном n-1 и выходным валом привода звена n заменяем реакциями
и
и составляем кинетостатические векторные уравнения равновесия сил и моментов для звена n (Рис.20.4):
где
- вектор момента в кинематической паре (проекция этого вектора на ось z является движущим моментом привода в КП, то есть
).
Проецируя векторные уравнения на оси координат, получим систему шести алгебраических уравнений откуда определим шесть неизвестных
Далее рассматривается равновесие звена n-1. При этом в месте его присоединения к звену n прикладываются реакции со стороны звена n
,
равные по величине и противоположные по направлению реакциям, определенным на предыдущем этапе расчета. Так последовательно составляются уравнения силового равновесия для всех n звеньев механизма. Из решения полученной системы 6n уравнений определяются реакции в кинематических парах, движущие силы и моменты.
Расчет быстродействия промышленного робота.
Время выполнения роботом цикла перемещений детали во многом определяет производительность всего роботизированного комплекса. Поэтому требования к быстродействию робота обычно достаточно высокие. Время выполнения роботом технологической операции обусловлено законами изменения внешних сил (движущих и сопротивления) и инертностью звеньев механизма. Закон изменения управляющих сил зависит от типа используемого привода и от вида системы управления. Существуют роботы с гидравлическими, пневматическими, электрическими и комбинированными приводами. В них применяются цикловые, позиционные или контурные системы управления. Рассмотрим расчет быстродействия одного из приводов промышленного робота с цикловой системой управления. При цикловой системе управления относительные перемещения звеньев ограничиваются передвижными упорами и концевыми выключателями.
На рис. 20.5 изображена кинематическая схема трехподвижного манипулятора ПР (1,2,3 – подвижные звенья, 0 – неподвижное звено). Здесь же приведена циклограмма настройки командоаппарата (сплошные линии) и циклограмма работы ПР (пунктирные линии). Общее время рабочего цикла Тц состоит из времени выстоя в заданных положениях (на циклограмме выстой показан прямыми параллельными горизонтальной оси t) и времени относительных перемещений звеньев из одного заданного положения в другое tпх и обратно tох (наклоные прямые на диаграммах ). Время выстоя обычно задано условиями технологического процесса. Время выполнения роботом движений определяется динамическими характеристиками приводов и манипулятора – движущими силами и силами сопротивления, массами и моментами инерции звеньев.
Циклограммы командоаппарата и промышленного робота.
Рассмотрим работу пневмопривода перемещения руки манипулятора (рис.20.5). По сигналу от командоаппарата в правую полость цилиндра подается сжатый воздух, который действует на поршень с силой
Fд3 = p * Sп, где р - давление воздуха, Sп - активная площадь поршня. Под действием этой силы поршень и рука 3 перемещаются влево с постоянным ускорением и с возрастающей скоростью V32 (рис.20.6а). Ограничение хода поршня может осуществляться либо жестким упором без демпфера, либо упором с демпфером.
При остановке на упоре без демпфера , скорость звена 3 должна мгновенно уменьшится с некоторого конечного значения до нуля. При таком изменении скорости ускорение a32 стремится к бесконечности. Такая остановка звена называется жестким ударом. Она сопровождается большими динамическими нагрузками на звенья механизма. Так как реальный манипулятор представляет собой упруго-инерционную систему, то эти нагрузки вызовут отскок звена 3 от упора, а также колебания всего механизма. Схват будет совершать колебания относительно заданного конечного положения. Время затухания этого процесса Dt (рис.20.6а) значительно снижает быстродействие ПР.
Уменьшить эти колебания или вообще исключить их можно, обеспечив безударный останов
V32n = 0, a32n = 0;
где V32n, a32n - относительная скорость и относительное ускорение звеньев в момент останова. Однако это осуществимо только в регулируемом приводе при контурном управлении. Кроме того при безударном останове в конце хода относительная скорость близка к нулю, поэтому время перемещения схвата в требуемое положение значительно возрастает. Компромиссным решением является останов с мягким ударом, при котором относительная скорость в конце хода V32n= 0, а ускорение ограничено некоторым допустимым значением a32n . В механизмах с цикловым управлением режим движения с мягким ударом обеспечивается установкой упоров с демпферами, гасящими кинетическую энергию руки.
Расчет демпфера ведется из условия ASn =0 , которое обеспечивается равенством за цикл движения работы движущей силы AFд3 и работы силы сопротивления демпфера АFc (рис. 20.6б):
AFд3 = -АFc
или Fд3 * (H32 – hд) = - Fc * hд.
В этом выражении неизвестны две величины Fc и hд, одной из них задаются, вторую – рассчитывают.
Уравновешивание манипуляторов.
В большинстве кинематических схем манипуляторов приводы восприниамают статические нагрузки от сил веса звеньев. Это требует значительного увеличения мощностей двигателей приводов и моментов тормозных устройств. Для борьбы с этим используют три метода:
Используют кинематические схемы манипуляторов, в которых силы веса звеньев воспринимаются подшипниками кинематических пар. На мощность приводов и тормозных устройств при таком решении силы веса оказывают влияние только через силы трения в парах. В качестве примера можно привести кинематическую схема робота SCARA (рис. 20.7). Недостатком этого метода являются большие осевые нагрузки в подшипниках.
Уравновешивание звеньев манипулятора с помощью корректировки их массы. При этом центр масс звена с помощью корректирующих масс смещается в центр кинематической пары ( рис. 20.8 ). Недостатком этого метода является значительное увеличение массы манипулятора и моментов инерции его звеньев.
Уравновешивание сил веса звеньев манипулятора с помощью упругих разгружающих устройств – пружинных разгружателей или уравновешивателей. Эти устройства не позволяют обеспечить полную разгрузку приводов от действия сил веса на всем относительном перемещении звеньев. Поэтому конструкция этих устройств включает кулачковые или рычажные механизмы, которые согласуют упругую характеристику пружины с характеристикой уравновешиваемых сил веса звеньев. На рис. 20.9 показана схема примышленного робота в котором привод вертикального перемещения руки снабжен механизмом для силовой разгрузки, состоящим из пружины и кулачкового механизма с профилем выполненным по спирали Архимеда.
Точность манипуляторов ПР.
Точность манипуляторов определяется погрешностями позиционирования характеристической точки схвата (точка М) и погрешностями угловой ориентации схвата. Погрешности позиционирования определяются технологическими отклонениями размеров звеньев манипулятора, зазорами в кинематических парах манипулятора и механизмов приводов, деформациями (упругими и температурными) звеньев, а также погрешностями системы управления и датчиков обратной связи. В паспортных данных манипуляторов указывается максимально допустимое отклонение центра схвата манипулятора точки М от ее номинального расположения на множестве возможных конфигураций механизма. В результате погрешностей точка М
описывает в пространстве некоторый эллипсоид, который называется эллипсоидом отклонений (рис. 20.10).
Литература
Силовой расчет, уравновешивание, проектирование механизмов и механика манипуляторов: Учебное пособие для студентов смешанной формы обучения / И.Н.Чернышева, А.К.Мусатов,Н.А.Глухов и др.; Под ред. А.К.Мусатова. – М.: Изд-во МГТУ, 1990. – 80с., ил.
Механика промышленных роботов: Учеб. пособие для втузов: В 3-х кн. / под ред. К.В.Фролова, Е.И.Воробьева. – М.: Высш.шк., 1988.
Р.Пол “Моделирование, планирование траекторий и управление движением робота – манипулятора” - М.: Наука, 1976.
Зубчатые передачи с зацеплением М.Л.Новикова
Краткое содержание:
Зубчатые передачи с зацеплением М.Л.Новикова.
Конические зубчатые передачи.
Червячные зубчатые передачи.
Зубчатые передачи с циклоидальными профилями
Зубчатые передачи с зацеплением М.Л.Новикова
С целью повышения несущей способности зубчатых передач М.Л.Новиков [1] разработал новый способ образования сопряженных поверхностей для различных видов зубчатых передач с параллельными, пересекающимися и перекрещивающимися осями. До Новикова исходили из того, что в передачах с параллельными осями поверхности зубьев находятся в линейном контакте, а их торцевые профили являются взаимоогибаемыми кривыми. Новиков предложил перейти от линейного контакта поверхностей к точечному. При этом профили зубьев в торцевом сечении могут быть не взаимоогибаемыми кривыми и их можно выполнять как выпуклый и вогнутый профили с малой разностью кривизн. В передаче с параллельными осями линия зацепления является прямой линией параллельной осям колес. Зацепление Новикова имеет только осевое перекрытие :
где b - ширина зубчатого венца, pz - осевой шаг. Поэтому поверхности зубьев выполняются винтовыми (косозубыми) с углом подъема винтовой линии
Одним из основных параметров зацепления Новикова является расстояние от полюса зацепления Р до точки контакта К, которое определяет положение линии зацепления ( прямой К-К параллельной осям вращения и проходящей через точку контакта К ) относительно оси мгновенного относительного вращения Р-Р. Согласно рекомендациям работы [ 14.1 ], это расстояние выбирается в зависимости от величины передаваемой мощности в пределах
Радиусы кривизны рабочих участков профилей рекомендуется выбирать для выпуклой поверхности
,для вогнутой поверхности
, где k2 = 0.03 ... 0.1 .
Радиус окружности вершин колеса с выпуклыми зубьями:
где
Дуги рабочих профилей выпуклых зубьев проводят от начальной окружности до окружности вершин. Радиус окружности вершин колеса с вогнутыми зубьями .
где
- глубина захода зубьев.
Радиус окружности впадин колеса с выпуклыми зубьями:
где c - радиальный зазор, приблизительно равный
Радиус окружности впадин колеса с вогнутыми зубьями :
где
- межосевое расстояние в передаче .
Преимущества зубчатых передач с зацеплением Новикова:
повышенная контактная прочность зубьев, за счет использования зацепления вогнутого профиля с выпуклым ( приведенный радиус кривизны определяется суммой радиусов кривизны профилей );
перекрытие в передачах Новикова обеспечивается только за счет осевого перекрытия, поэтому высота зубьев может быть достаточно малой, что обеспечивает высокую изгибную прочность зубьев ( в целом, по приблизительным оценкам, нагрузочная способность передач Новикова в 2-3 раза выше, чем косозубых эвольвентных передач с одинаковыми размерами);
точечное зацепление (пятиподвижная кинематическая пара) обеспечивает в передачах с зацеплением Новикова меньшую чувствительность к монтажным погрешностям.
К недостаткам передач Новикова можно отнести
более сложную технологию изготовления, за счет использования инструмента с профилями криволинейной конфигурации;
наличие значительных осевых нагрузок на подшипники из-за использования винтовых зубьев с большими углами подъема винтовой линии;
склонность зубьев винтовых колес к излому у торца при входе в зацепление
Конические зубчатые передачи.
Конической называется зубчатая передача, предназначенная для передачи и преобразования вращательного движения между звеньями, оси вращения которых пересекаются.
Схема конической передачи представлена на рис. 14.2. Оси колес зубчатой передачи пересекаются в точке 0. Угол Е между осями колес ( или между векторами угловых скоростей звеньев w1 и w2 ) называется межосевым углом. Этот угол может изменяться в пределах 0° < Е < 180°. При Е= 0° передача превращается в цилиндрическую с внешним зацеплением, а при E= 180° - в цилиндрическую с внутренним зацеплением. Таким образом, коническая передача является общим случаем зубчатой передачи, нежели цилиндрические. Начальные или аксоидные поверхности в конической передаче имеют форму конусов.
Аксоидными называются поверхности, которые образуются осями мгновенного относительного вращения колес, в системах координат связанных с колесами ( звеньями передачи ). Если колеса передачи обработаны без смещения исходного контура, то аксоидные поверхности совпадают с делительными. При относительном движении аксоиды перекатываются друг по другу, при этом скольжение возможно только в направлении оси относительного вращения. Поэтому вектора угловых скоростей звеньев связаны между собой векторным уравнением
если известна величина w1, то из этого уравнения можно определить w1 и w2. Из векторного треугольника D a0b
Передаточное отношение конической передачи
Так как
тo
Тогда углы начальных ( делительных при х=0 ) конусов
Геометрия зацепления в конической зубчатой передаче:
Как и в цилиндрических, так и в конических зубчатых передачах наиболее часто применяют эвольвентное зацепление. Эвольвентная поверхность зуба конического колеса образуется при перекатывании производящей плоскости по основному конусу. Эвольвентные кривые формируются на соосных сферических поверхностях с центром в вершине основного конуса. Поэтому для расчета геометрии эвольвентной конической передачи необходимо применять сферическую геометрию. Так как это сложно, то используют приближенный метод расчета геометрии - метод дополнительных конусов [2], предложенный английским столяром Томасом Тредгольдом. При этом методе расчет геометрии проводится для эквивалентного цилиндрического зацепления двух секторов. Эти сектора образуются развертками конусов, которые построены на внешней сфере радиуса R we . Радиусы оснований этих конусов r we1 = r e1 и r we2 = r e2 , а образующие являются касательными к сфере (рис.14.3). Числа зубьев колес эквивалентного цилиндрического зацепления рассчитываются на основании следующих формул
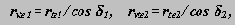
где rte1и rte2 - радиусы торцевых делительных окружностей на внешней сфере, rvte1и rvte2- радиусы делительных окружностей эквивалентного цилиндрического зацепления.
Так как

то :
где z1 и z2 - числа зубьев колес конической передачи, zvt1 и zvt2 - числа зубьев колес эквивалентного цилиндрического расчетного зацепления ( эти величины могут быть дробными).
После определения чисел зубьев эквивалентного цилиндрического зацепления, приближенный расчет геометрических параметров для внешнего торца конического зацепления можно проводить по рассмотренным выше формулам цилиндрического эвольвентного зацепления. Радиус внешней сферы (длина образующей начального или делительного конуса)
Ширина зубчатого венца
, где b=0.3....0.4 - коэффициент ширины зубчатого венца.
По форме линии зуба конические зубчатые передачи различаются на: прямозубые; косозубые; с круговым зубом; с эвольвентной линией зуба; с циклоидальной линией зуба
Преимущества и недостатки кинических зубчатых передач.
Преимущества:
обеспечение возможности передачи и преобразования вращательного движения между звеньями с пересекающимися осями вращения;
возможность передачи движения между звеньями с переменным межосевым углом при широком диапазоне его изменения;
расширение компоновочных возможностей при разработке сложных зубчатых и комбинированных механизмов.
Недостатки:
более сложная технология изготовления и сборки конических зубчатых колес;
большие осевые и изгибные нагрузки на валы, особенно в связи с консольным расположением зубчатых колес.
Червячные зубчатые передачи.
Червячной - называется зубчатая передача, состоящая из двух подвижных звеньев - червяка и зубчатого колеса и предназначенная для передачи и преобразования вращательного движения между ортагональными перекрещивающимися осями. Червяком называют звено, наружная поверхность которого имеет форму винта. Червячным колесом называется зубчатое колесо с косыми зубьями, которое зацепляется с червяком
Виды червячных передач и червяков ( по ГОСТ 18498-73 ).
по виду делительной поверхности червяка
цилиндрические червячные передачи - червяк и колесо в передаче имеют цилиндрические делительные и начальные поверхности;
глобоидные червячные передачи - делительная и начальная поверхности червяка образованы вращением отрезка дуги делительной или начальной поверхности парного червячного колеса вокруг оси червяка;
по виду теоретического торцового профиля витка червяка
архимедов червяк (ZA) - профиль выполнен по архимедовой спирали;
эвольвентный червяк (ZI) - профиль выполнен по эвольвенте окружности;
конволютный червяк (ZN) - профиль выполнен по удлиненной эвольвенте
Геометрия зацепления цилиндрической червячной передачи
Расчет геометрии зацепления цилиндрической червячной передачи регламентируется ГОСТ 19650 - 74 [3]. Связь между основными параметрами червяка - диаметром начального цилиндра d w1 , ходом винтовой линии pz1 и углом ее наклона bw - устанавливается следующим соотношением
Связь между ходом винтовой линии pz1 и шагом многозаходного винта p1
Расчет геометрии зацепления.
Исходные данные:
m - модуль осевой; q - коэффициент диаметра червяка; z1 - число витков червяка; aw - межосевое расстояние; x - коэффициент смещения червяка; u - передаточное число.
Параметры инструмента:
h* = (h*w + c*1) - коэффициент высоты витка; h*a - коэффициент высоты головки; s* - коэффициент расчетной толщины; r*f - коэффициент радиуса кривизны переходной кривой;
c*1,2 = 0.25 … 0.5 ; s* = 0.75 Ч p ; r*f = 0.3 … 0.45 .
Расчет геометрических параметров.
Число зубьев колеса
Коэффициент смещения ( если задано межосевое расстояние )
Межосевое расстояние ( если задан коэффициент смещения )
Делительные диаметры
Начальные диаметры
Делительный угол подъема витка червяка
Начальный угол подъема витка червяка
Основной угол подъема витка червяка ( только для червяков ZI )
и основной диаметр червяка
Высота витка червяка
Высота головки витка червяка
Диаметры вершин витков червяка
зубьев червячного колеса в средней торцовой плоскости
Диаметры впадин червяка
червячного колеса
Наибольший диаметр червячного колеса
Ширина венца червячного колеса
Длина нарезанной части червяка ( при х= 0 )
Геометрические показатели качества зацепления.
Подрезание зубьев червячного колеса отсутствует если
Заострение зубьев в средней торцовой плоскости отсутствует, если
Заострение зубьев в средней торцовой плоскости отсутствует, если
Преимущества и недостатки червячных зубчатых передач
Преемущества:
благодаря малому числу заходов червяка (z1= 1…4) червячная передача позволяет реализовывать в одной ступени большие передаточные отношения;
обладает высокой плавностью, низким уровнем вибраций и шума;
позволяет обеспечить самоторможение червячного колеса ( при малых углах подъема витка передача движения от вала червячного колеса к червяку становится невозможной)
Недостатки:
высокая скорость скольжения вдоль линии зуба, что ведет к повышенной склонности к заеданию ( необходимы специальные смазки и материалы для зубчатого венца червячного колеса ), снижению КПД и более высокому тепловыделению .
Зубчатые передачи с циклоидальными профилями
Циклоидальными кривыми или циклоидами (рулеттами, трохоидами)
называется семейство кривых, которые описываются точками окружности или точками, связанными с этой окружностью, при ее перекатывании без скольжения по другой окружности или прямой [4]. Пусть образующая циклоиду точка лежит на окружности, тогда описываемая ей траектория будет эпициклоидой при внешнем контакте окружностей, гипоциклоидой - при внутреннем, или просто циклоидой - при перекатывании по прямой. Если образующая точка лежит вне окружности или внутри нее, то описываемые ей циклоидальные траектории называются эпитрахоидами (удлиненными или укороченными эпициклоидами) при внешнем контакте окружностей, гипотрохоидами (удлиненными или укороченными гипоциклоидами) - при внутреннем.
Теорема Камуса.
Теорема Камуса доказывает что профили выполненные по циклоидальным кривым будут при определенных условиях сопряженными и взаимоогибаемыми. Теорема Камуса. Кривые, описываемые какой-либо точкой жестко связанной с некоторой вспомогательной центроидой при перекатывании ее по центроидам, определяющим относительное движение рассматриваемых звеньев, будут взаимоогибаемыми в относительном движении этих звеньев.
Рассмотрим схему изображенную на рис. 14.7. На этой схеме: Ц1-Ц1 и Ц2-Ц2 - центроиды, определяющие движение звеньев 1 и 2; Ц3-Ц3 - вспомогательная центроида, с которой жестко связана кривая М-М; К1-К1 - огибающая к положениям М-М при перекатывании Ц3-Ц3 и Ц1-Ц1; К2-К2 - огибающая к положениям М-М при перекатывании Ц3-Ц3 и Ц2-Ц2; К1-К1 и К2-К2 - взаимоигибаемые кривые в относительном движении звеньев 1 и 2; дуга РР1 = дуге РР2 = дуге РР3; М'Р3 - нормаль к М-М из точки Р3;
Через промежуток времени dt точки Р1, Р2 и Р3 совпадут Р, касательные и прямые М'P3, K'2P2 и K'1P1 сольются в одну, то есть точки K'2 и K'1 образуют контактную точку K, а прямые проходящие через нее и полюс Р (K'2P2 и K'1P1), согласно с требованиями теоремы Виллиса, образуют контактную нормаль. Рассмотрим схему зубчатой передачи с циклоидальным зацеплением, которая изображена на рис. 14.8.
На этой схеме: rw1 и rw2 - радиусы начальных окружностей (центроид в относительном движении зубчатых колес), rv1 и rv2 - радиусы вспомогательных окружностей, точки которых образуют эпициклоиды Рa и гипоциклоиды Рb, используемые в качестве профилей при формировании зубьев.

Профиль головки зуба колеса 1 очерчен по эпициклоиде Рa , а профиль ножки по гипоциклоиде Рbў . На колесе 2 аналогично для профиля головки зуба используется эпициклоида Рaў , а для ножки - гипоциклоида Рb. Эпициклоиды Рa и Рaў получены при перекатывании вспомогательной окружности rv1 соответственно по начальным окружностям rw1 и rw2 . Гипоциклоиды Рb и Рbў получены при перекатывании вспомогательной окружности rv2 соответственно по начальным окружностям rw1 и rw2 . Геометрическое место точек контакта профилей в неподвижной системе координат - линия зацепления K1K2, образуется отрезками дуг вспомогательных окружностей PK1 и PK2 . Коэффициент перекрытия ea = (PK1 + PK2)/pw , где pw - шаг по начальной окружности rw1 ( или rw2 ). Исходный производящий контур реечного инструмента, используемый для обработки циклоидальных зубчатых колес образован двумя дугами циклоидальных кривых. Для нарезания двух колес необходимо иметь два инструмента с одним исходным производящим контуром, которые конгруентны друг другу (как шаблон и контршаблон).
Преимущества и недостатки циклоидального зацепления
Преемущества:
меньший износ профилей за счет использования зацепления выпуклого профиля с вогнутым;
больший, чем в аналогичной эвольвентной передаче, коэффициент перекрытия;
возможность получения на шестерне (трибе) без подрезания меньшего числа зубьев, нежели в эвольвентных зубчатых передачах;
меньшая скорость скольжения профилей
Недостатки:
более сложный профиль режущего инструмента, а следовательно, и большая стоимость изготовления;
чувствительность к монтажным погрешностям межосевого расстояния (изменение межосевого расстояния изменяет передаточное отношение).
Примечание: К разновидностям циклоидальных зацеплений относятся часовое и цевочное.В часовом зацеплении радиус вспомогательной окружности выбирается равным половине радиуса соответствующей начальной окружности. Тогда гипоциклоиды, образующие ножки зубьев, вырождаются в прямые линии. В цевочном зацеплении радиус вспомогательной окружности цевочного колеса принимают равным радиусу начальной окружности этого колеса. Профиль зуба цевочного колеса - окружность, а профиль зуба второго колеса - эквидистанта к эпициклоиде.